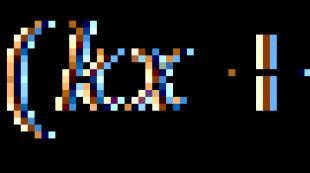Законы Бойля – Мариотта, Гей-Люссака, Шар­ля. Закон Бойля-Мариотта. Газовые законы. Изотерма Необходимость применения закона бойля мариотта

При постоянной температуре объем, занимаемый газом, обратно пропорционален его давлению.

Роберт Бойль — яркий пример ученого-джентльмена, сына давно ушедшей эпохи, когда наука была уделом исключительно состоятельных людей, посвящавших занятиям ею свой досуг. Большинство исследований Бойля относятся по современной классификации к разряду химических опытов, хотя сам себя он, наверняка, считал натурфилософом (физиком-теоретиком) и естествоиспытателем (физиком-экспериментатором). Судя по всему, поведением газов он заинтересовался, увидев проект одного из первых в мире воздушных насосов. Сконструировав и построив очередную, усовершенствованную версию своего двустороннего воздушно-вакуумного насоса, он решил исследовать, как повышенное и пониженное давление газа в герметичном сосуде, к которому был подключен его новый аппарат, влияет на свойства газов. Будучи одаренным экспериментатором, Бойль одновременно придерживался весьма новых и необычных для той эпохи взглядов, считая, что наука должна идти от эмпирических наблюдений, а не основываться исключительно на умозрительно-философских построениях.

В формулировке Бойля закон звучал буквально так: «Под воздействием внешней силы газ упруго сжимается, а в ее отсутствие расширяется, при этом линейное сжатие или расширение пропорционально силе упругости газа». Представьте, что вы сдавливаете надутый воздушный шарик. Поскольку свободного пространства между молекулами воздуха достаточно, вы без особого труда, приложив некоторую силу и проделав определенную работу, сожмете шарик, уменьшив объем газа внутри него. Это одно из основных отличий газа от жидкости. В шарике с жидкой водой, например, молекулы упакованы плотно, как если бы шарик был заполнен микроскопическими дробинками. Поэтому вода не поддается, в отличие от воздуха, упругому сжатию. (Если не верите, попробуйте протолкнуть плотно пригнанную пробку внутрь горлышка бутылки, заполненной водой по самую пробку.) Закон Бойля—Мариотта , наряду с законом Шарля , лег в основу Уравнения состояния идеального газа .

Дж. Трефил называет его «закон Бойля», однако мы предпочли принятое в российской традиции название закона. — Прим. переводчика .

См. также:

Robert Boyle, 1627-91

Англо-ирландский физик и химик. Родился в замке Лисмор (Lismore Castle), Ирландия, став четырнадцатым ребенком графа Коркского (Earl of Cork) — знаменитого авантюриста эпохи королевы Елизаветы. Окончив привилегированную Итонскую школу, где был одним из первых учеников среди «юных джентльменов», отправился в многолетнее путешествие по континентальной Европе, в ходе которого продолжил образование в Женевском университете. Вернувшись на родину в 1648 году, оборудовал частную лабораторию и занялся на ее базе физико-химическими исследованиями. В 1658 году перебрался в Оксфорд, где его учеником и ассистентом по лаборатории стал Роберт Гук (см. Закон Гука), будущий научный секретарь Королевского общества. Кстати, Бойль был одним из основателей и соучредителей Королевского общества, выросшего из кружка молодых оксфордских ученых. Провел целый ряд новаторских химических экспериментов, включая эксперименты по детальному изучению свойств кислот и оснований . По некоторым данным, первым выдвинул гипотезу о существовании химических элементов. Доказал, что воздух необходим для горения и дыхания. Помимо занятий наукой был соучредителем и членом-пайщиком «Восточно-индийской компании» и активно занимался миссионерской деятельностью в надежде обратить в христианство жителей восточных колоний Британской империи.

Основные законы идеальных газов используются в технической термодинамике для решения целого ряда инженерно-технических задач в процессе разработки конструкторско-технологическойдокументации авиационной техники, авиадвигателей; их изготовления и эксплуатации.

Эти законы первоначально были получены экспериментальным путем. В последующем они были выведены из молекулярно-кинетической теории строения тел.

Закон Бойля – Мариотта устанавливает зависимость объема идеального газа от давления при постоянной температуре. Эту зависимость вывел английский химик и физик Р. Бойль в 1662 году задолго до появления ки­нетической теории газа. Независимо от Бойля в 1676 го­ду этот же закон открыл Э. Мариотт. Закон Роберта Бойля (1627 – 1691), английского химика и физика, установившего этот закон в 1662 году, и Эдма Мариотта (1620 – 1684),французского физика, установившего этот закон в 1676 году: произведение объёма данной массы идеального газа на его давление постоянно при постоянной температуре или.

Закон получил на­звание Бойля – Мариотта и утверждает, что при посто­янной температуре давление газа обратно пропорцио­нально его объему .

Пусть при постоянной температуре некоторой массы газа имеем:

V 1 – объем газа при давлении р 1 ;

V 2 – объем газа при давлении р 2 .

Тогда согласно закону мож­но записать

Подставив в это уравнение значение удельного объема и принимая массу данного газа т = 1кг, полу­чим

p 1 v 1 =p 2 v 2 илиpv = const .(5)

Плотность газа – величина, обратная его удельному объему:

тогда уравнение (4) примет вид

т. е. плотности газов прямо пропорциональны их абсо­лютным давлениям. Уравнение (5) можно рассматривать как новое выражение закона Бойля – Мариотта которое можно сформулировать так: произведение давления на удельный объем определенной массы одного и того же идеального газа для различных его состояний, но при одинаковой температуре, есть величина постоянная .

Этот закон может быть легко получен из основного уравнения кинетической теории газов. Заме­нив в уравнении (2) число молекул в единице объема отношением N /V (V – объем данной массы газа, N – число молекул в объеме) получим

Поскольку для данной массы газа величины N и β постоянны, то при постоянной температуре T =const для произвольного количества газа уравнение Бойля – Мариотта будет иметь вид

pV = const , (7)

а для 1 кг газа

pv = const .

Изобразим графически в системе координат р – v из­менение состояния газа.

Например, давление данной массы газа объемом 1 м 3 равно 98 кПа, тогда, используя уравнение (7), определим давление газа объемом 2 м 3

Продолжая расчеты, получим следующие данные: V (м 3) равно 1; 2; 3; 4; 5; 6; соответственно р (кПа) равно 98; 49; 32,7; 24,5; 19,6; 16,3. По этим данным строим график (рис. 1).

Рис. 1. Зависимость давленияидеального газа от объема при

постоянной температуре

Полученная кривая – гипер­бола, полученная при пос­тоянной температуре, назы­вается изотермой, а процесс, протекающий при постоян­ной температуре, – изотер­мическим. Закон Бойля – Мариотта – приближенный и при очень больших дав­лениях и низких темпера­турах для теплотехнических расчетов неприемлем.

Закон Г е й – Л ю с с а к а определяет зависимость объ­ема идеального газа от температуры при постоян­ном давлении. (Закон Жозефа Луи Гей-Люссака (1778 – 1850), французского химика и физика, установившего впервые этот закон в 1802 году: объём данной массы идеального газа при постоянном давлении линейно возрастает с ростом температуры , то есть, где - удельный объём при; β – коэффициент объёмного расширения равный 1/273,16 на 1 о С.) Закон уста­новлен экспериментально в 1802 г. французским физи­ком и химиком Жозефом Луи Гей-Люссаком, именем которого назван. Исследуя на опыте тепловое расширение газов, Гей-Люссак от­крыл, что при неизменном давлении объемы всех газов увеличиваются при нагревании почти одинаково, т. е. при повышении температуры на 1°С объем некоторой массы газа увеличивается на 1/273 объема, который дан­ная масса газа занимала при 0°С.

Увеличение объема при нагревании на 1 °С на одну и ту же величину не случайно, а как бы является след­ствием закона Бойля – Мариотта. Вначале газ нагрева­ется при постоянном объеме на 1 °С, давление его увели­чивается на 1/273 начального. Затем газ расширяется при постоянной температуре, причем его давление уменьшается до начального, а объем во столько же раз увеличи­вается. Обозначив объем некоторой массы газа при 0°С через V 0 , а при температуре t °C через V t запишем закон следующим выражением:

Закон Гей-Люссака также можно изобразить графи­чески.

Рис. 2. Зависимость объема идеального газа от температу­ры при постоянном

давлении

Используя уравнение (8) и принимая температуру равной 0°С, 273 °С, 546 °С, вычислим объем газа, равный соответственно V 0 , 2V 0 , 3V 0 . Отложим по оси абсцисс в некотором условном масштабе (рис. 2) температуры га­за, а по оси ординат – соответствующие этим темпера­турам объемы газа. Соединяя на графике полученные точки, получим прямую, представляющую собой график зависимости объема идеального газа от температуры при постоянном давлении. Такая прямая называется изобарой , а процесс, протекающий при постоянном дав­лении – изобарным .

Обратимся еще раз к графику изменения объема га­за от температуры. Продолжим прямую до пересечения, с осью абсцисс. Точка пересечения будет соответствовать абсолютному нулю.

Предположим, что в уравнении (8) значение V t = 0, тогда имеем:

но так как V 0 ≠ 0, следовательно, откуда t = – 273°C. Но – 273°C=0К, что и требовалось дока­зать.

Представим уравнение Гей-Люссака в виде:

Помня, что 273+t =Т , а 273 К=0°С, получим:

Подставляя в уравнение (9) значение удельного объема и принимая т =1 кг, получим:

Отношение (10) выражает закон Гей-Люссака, кото­рый можно сформулировать так: при постоянном давле­нии удельные объемы одинаковых масс одного и того же идельного газа прямо пропорциональны его абсолютным температурам . Как видно из уравнения (10), закон Гей-Люссака утверждает, что частное от деления удельногообъема данной массы газа на его абсолютную темпера­туру есть величина постоянная при данном постоянном давлении .

Уравнение, выражающее закон Гей-Люссака, в об­щем виде имеет вид

и может быть получено из основного уравнения кине­тической теории газов. Уравнение (6) представим в виде

при p =const получаем уравнение (11). Закон Гей-Люссака широко применяется в технике. Так, на основе закона объемного расширения газов по­строен идеальный газовый термометр для измерения температур в пределах от 1 до 1400 К.

Закон Шарля устанавливает зависимость давле­ния данной массы газа от температуры при постоянном объеме.ЗаконЖана Шарля (1746 – 1823),французского ученого, установившего этот закон впервые в 1787 году, и уточненный Ж.Гей-Люссакомв 1802 году: давление идеального газа неизменной массы и объёма возрастает при нагревании линейно, то есть, где р о – давление приt = 0°C.

Шарль определил, что при нагревании в по­стоянном объеме давление всех газов увеличивается почти одинаково, т.е. при повышении температуры на 1 °С давление любого газа увеличивается точно на1/273 того давления, которая данная масса газа имела при 0°С. Обозначим давление некоторой массы газа в сосуде при 0°С через р 0 , а при температуре t ° через p t . При по­вышении температуры на 1°С давление увеличивается на, а при увеличении на t °Cдавление увеличива­ется на. Давление при температуре t °Cравно начальному плюс прирост давления или

Формула (12) позволяет вычислить давление при лю­бой температуре, если известно давление при 0°С. В инженерных расчетах очень часто используют уравнение (закон Шарля), которое легко получается из соотношения (12).

Поскольку, а 273 + t = Т или 273 К = 0°С = Т 0

При постоянном удельном объеме абсолютные давле­ния идеального газа прямо пропорциональны абсолют­ным температурам. Поменяв местами средние члены пропорции, получим

Уравнение (14) есть выражение закона Шарля в об­щем виде. Это уравнение легко вывести из формулы (6)

При V =const получаем общее уравнение закона Шарля (14).

Для построения графика зависимости данной массы газа от температуры при постоянном объеме воспользу­емся уравнением (13). Пусть, например, при температу­ре 273 К=0°С давление некоторой массы газа 98 кПа. По уравнению давление при температуре 373, 473, 573 °С соответственно будет 137 кПа (1,4 кгс/см 2), 172 кПа (1,76 кгс/см 2), 207 кПа (2,12 кгс/см 2). По этим данным строим график (рис. 3). Полученная прямая называется изохорой, а процесс, протекающий при постоянном объеме, – изохорным.

Рис. 3. Зависимость давления газа от темпера­туры при постоянном объеме

Согласно закону Бойля - Мариотта , при постоянной температуре объем газа обратно пропорционален давлению.

Это означает, что с ростом давления на газ его объем уменьшается, и наоборот. Для неизменного количества газа закон Бойля - Мариотта можяо также интерпретировать следующим образом: при неизменной температуре произведение давления на объем является величиной постоянной. В виде формулы это выражается так:

Р х V = К, где Р - абсолютное даатение, V - объем; К - константа.

Если Р и V меняются, то Р 1 х V 1 = К и Р 2 х V 2 = К.

Совмещение двух уравнений даст Р 1 х V 1 = Р 2 х V 2 .

Если фиксированное количество газа закачать в жесткую емкость, такую, как баллон акваланга, то, поскольку объем баллона остается неизменным, им и будет определяться давление газа внутри него. Если тем же количеством газа заполнить эластичную емкость, например воздушный шар. он будет расширяться, пока давление газа внутри него не сравняется с давлением окружающей среды. В данном случае давление определяет объем емкости.

Эффект от увеличения давления с глубиной погружения на примере пластиковой бутылки. По мере увеличения давления на газ его объем уменьшается, и наоборот

На уровне моря давление равно 1 бар. На глубине 10 метров давление удваивается до 2 бар и далее с каждыми 10 метрами погружения увеличивается на 1 бар. Представьте перевернутую стеклянную бутылку без пробки, внутри которой находится воздух. При погружении бутылки на глубину 10 метров, где давление составляет 2 бар. воздух внутри нее сожмется до половины своего первоначального объема. На глубине 20 метров давление будет равно 3 бар. а воздух сожмется до трети первоначального объема. На 30 метрах глубины, где давление возрастает до 4 бар. объем воздуха составит лишь четверть от первоначатыюго.

Если давление и объем газа - величины обратно пропорциональные, то давление и плотность прямо пропорциональны. С увеличением давления газа и уменьшением его объема расстояние между молекулами газа сокращается, и газ становится плотнее. При давлении, вдвое превышающем атмосферное, заданный объем газа вдвое плотнее воздуха у поверхности воды и т. д. Поэтому на глубине дайверы быстрее расходуют имеющийся у них запас воздуха. Полный вдох воздуха, давление которого вдвое превышает атмосферное, содержит вдвое больше молекул воздуха, чем воздух на поверхности. Поэтому при давлении в 3 атмосферы баллона хватит лишь на треть того времени, в течение которого человек мог бы пользоваться этим баллоном на поверхности.

Дайвер должен дышать воздухом, давление которого равно давлению окружающей водной среды. Только тогда независимо от глубины погружения будет обеспечиваться расширение воздуха до нормального объема легких. Регулятор воздуха представляет собой систему клапанов, снижающих давление сжатого в баллоне воздуха до давления воды на уровне легких дайвера. Дайверы не хотят понапрасну расходовать воздух в своем баллоне, поэтому регулятор сконструирован так. чтобы подавать воздух только тогда, когда это нужно. Отсюда другое название - «demand valve». то есть клапан, срабатывающий по требованию.

При каждом погружении дайверы несут на себе различные элементы снаряжения, содержащие газ, включая устройства для контроля плавучести, баллоны, маски, «мокрые» и «сухие» неопреновые гидрокостюмы из материала, содержащего его крошечные пузырьки воздуха. В нашем теле также есть наполненные газом полости: пазухи, уши. желудок и легкие. За исключением жестких баллонов, все газонаполненные полости сжимаются при погружении и расширяются при всплытии. При подъеме к поверхности дайверы должны освобождаться от расширяющегося в легких воздуха, выравнивать давление в ушах и пазухах во избежание боли и повреждения тканей, именуемого баротравмой. (Это не касается декомпрессионных остановок - о них разговор особый.)

Считается, что расширение газов в организме дайвера идет особенно интенсивно на последних 10 метрах подъема, вот почему на этом этапе подниматься следует медленно, постепенно выдыхая воздух.

Состав морской воды

Среди химических соединений, придающих морской воде ее соленый вкус, преобладает поваренная соль (хлорид натрия). В среднем в морской воде содержится примерно 3% соли, хотя этот показатель может варьироваться от 1% в полярных морях до 5% в замкнутых, таких, как Средиземное и Красное. Соль, получаемая при выпаривании морской воды, на 77,76% состоит из хлорида натрия, на 10,88% - из хлорида магния, на 4,74% - из сульфата магния, на 3,60% - из сульфата кальция, на 2,46% - из хлорида калия, на 0,22% - из бромида магния и на 0,34% из карбоната кальция.

ОПРЕДЕЛЕНИЕ

Процессы, при которых один из параметров состояния газа остается постоянным называют изопроцессами .

ОПРЕДЕЛЕНИЕ

Газовые законы - это законы, описывающие изопроцессы в идеальном газе.

Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.

Рассмотрим каждый из них.

Закон Бойля-Мариотта (изотермический процесс)

Изотермическим процессом называют изменение состояния газа, при котором его температура остаётся постоянной.

Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:

Этот же закон можно переписать в другом виде (для двух состояний идеального газа):

Этот закон следует из уравнения Менделеева - Клапейрона:

Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.

Графики зависимости параметров газа при постоянной температуре называются изотермами .

Обозначив константу буквой , запишем функциональную зависимость давления от объема при изотермическом процессе:

Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах и соответственно.

Рис.1. Графики изотермических процессов в различных координатах

Закон Гей-Люссака (изобарный процесс)

Изобарным процессом называют изменение состояния газа, при котором его давление остаётся постоянным.

Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:

Этот закон также следует из уравнения Менделеева - Клапейрона:

изобарами .

Рассмотрим два изобарных процесса с давлениями и title="Rendered by QuickLaTeX.com" height="18" width="95" style="vertical-align: -4px;">. В координатах и изобары будут иметь вид прямых линий, перпендикулярных оси (рис.2 а,б).

Определим вид графика в координатах .Обозначив константу буквой , запишем функциональную зависимость объема от температуры при изобарном процессе:

Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.

Рис.2. Графики изобарных процессов в различных координатах

Закон Шарля (изохорный процесс)

Изохорным процессом называют изменение состояния газа, при котором его объем остаётся постоянным.

Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:

Для двух состояний газа этот закон запишется в виде:

Этот закон также можно получить из уравнения Менделеева - Клапейрона:

Графики зависимости параметров газа при постоянном давлении называются изохорами .

Рассмотрим два изохорных процесса с объемами и title="Rendered by QuickLaTeX.com" height="18" width="98" style="vertical-align: -4px;">. В координатах и графиками изохор будут прямые, перпендикулярные оси (рис.3 а, б).

Для определения вида графика изохорного процесса в координатах обозначим константу в законе Шарля буквой , получим:

Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).

Рис.3. Графики изохорных процессов в различных координатах

Примеры решения задач

ПРИМЕР 1

Задание	До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой , чтобы объем газа уменьшился при этом на одну четверть?
Решение	Изобарный процесс описывается законом Гей-Люссака: По условию задачи объем газа вследствие изобарного охлаждения уменьшается на одну четверть, следовательно: откуда конечная температура газа: Переведем единицы в систему СИ: начальная температура газа . Вычислим:
Ответ	Газ нужно охладить до температуры .

ПРИМЕР 2

Задание	В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30%?
Решение	Так как сосуд с газом закрытый, объем газа не меняется. Изохорный процесс описывается законом Шарля: По условию задачи температура газа повысилась на 30%, поэтому можно записать: Подставив последнее соотношение в закон Шарля, получим: Переведем единицы в систему СИ: начальное давление газа кПа= Па. Вычислим:
Ответ	Давление газа станет равным 260 кПа.

ПРИМЕР 3

Задание	В кислородной системе, которой оборудован самолет, имеется кислорода при давлении Па. При максимальной высоте подъема летчик соединяет с помощью крана эту систему с пустым баллоном объемом . Какое давление установится в ней? Процесс расширения газа происходит при постоянной температуре.
Решение	Изотермический процесс описывается законом Бойля-Мариотта:

Закон Бойля-Мариотта (Изотерма) , один из основных газовых законов, который описывает изотермические процессы в идеальных газах. Его установили учёные Р. Бойль в 1662 г. и Э. Мариотт в 1676 г. независимо друг от друга при экспериментальном изучении зависимости давления газа от его объема при постоянной температуре.

Согласно закону Бойля-Мариотта при постоянной температуре (Т=const), Объем (V) данной массы (m) идеального газа, обратно пропорционален его давлению (р):

pV = const = С при T=const и m=const

Постоянная С пропорциональна массе газа (числу молей) и его абсолютной температуре. Другими словами: произведение объема данной массы идеального газа на его давление постоянно при постоянной температуре. Закон Бойля -- Мариотта выполняется строго для идеального газа. Для реальных газов закон Бойля -- Мариотта выполняется приближенно. Практически все газы ведут себя как идеальные при не слишком высоких давлениях и не слишком низких температурах.

Закон Бойля -- Мариотта следует из кинетической теории газов, когда принимается допущение, что размеры молекул пренебрежимо малы по сравнению с расстоянием между ними и отсутствует межмолекулярное взаимодействие. При больших давлениях необходимо вводить поправки на силы притяжения между молекулами и на объем самих молекул. Как и уравнение Клайперона, закон Бойля -- Мариотта описывает предельный случай поведения реального газа, более точно описываемый уравнением Ван-дер-Ваальса. Применение закона приближенно можно наблюдать в процессе сжатия воздуха компрессором или в результате расширения газа под поршнем насоса при откачке его из сосуда.

Термодинамический процесс, который происходит при постоянной температуре называется изотермическим. Изображение его на графике (рис.1) называется изотермой.

Рис.1

Закон Гей-Люссака. Изобара

Французский ученый Ж. Гей-Люссак в 1802 году нашел экспериментально зависимость объема газа от температуры при постоянном давлении. Данные лежат в основе газового закона Гей-Люссака.

Формулировка закона Гей-Люссака следующая: для данной массы газа отношение объема газа к его температуре постоянно, если давление газа не меняется. Эту зависимость математически записывают так:

V/Т=const, если P=const и m=const

Данный закон приближенно можно наблюдать, когда происходит расширение газа при его нагревании в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня. Другим проявлением закона Гей-Люссака в действии является аэростат. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Закон справедлив для идеального газа. Он неплохо выполняется для разреженных газов, которые по своим свойствам близки к идеальному. Температура газа должна быть достаточно велика.

Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (рис.2 график изобарного процесса).

Рис.2

Закон Шарля. Изохора

Французский ученый Ж. Шарль в 1787 году нашел экспериментально зависимость давления газа от температуры при постоянном объеме. Данные лежат в основе газового закона Шарля.

Формулировка закона Шарля следующая: для данной массы газа отношение давления газа к его температуре постоянно, если объем газа не меняется. Эту зависимость математически записывают так:

P/Т=const, если V=const и m=const

Данный закон приближенно можно наблюдать, когда происходит увеличение давления газа в любой емкости или в электрической лампочке при нагревании. Изохорный процесс используется в газовых термометрах постоянного объема. Закон Шарля не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Закон справедлив для идеального газа. Он неплохо выполняется для разреженных газов, которые по своим свойствам близки к идеальному. Температура газа должна быть достаточно высокой. Процесс должен проходить очень медленно

Графически эта зависимость в координатах P-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным. Рис.3 (график изохорного процесса).