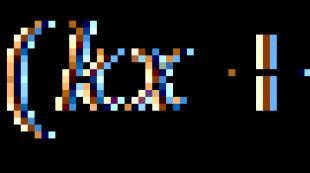Английский алфавит

Теория лобачевского о параллельных прямых. Пять мифов о геометрии лобачевского. Возникновение геометрии Лобачевского

Плоскость Лобачевского

Геометрия Лобачевского (гиперболическая геометрия ) - одна из неевклидовых геометрий , геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия , за исключением аксиомы о параллельных , которая заменяется на аксиому о параллельных Лобачевского .

Евклидова аксиома о параллельных гласит:

через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще.

История

Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида - аксиома, эквивалентная аксиоме о параллельных . Он входил в список постулатов в «Началах» Евклида). Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его из остальных постулатов Евклида.

Среди пытавшихся доказать были следующие учёные:

древнегреческие математики Птолемей (II в.), Прокл (V в.) (основывался на предположении о конечности расстояния между двумя параллельными),
Ибн аль-Хайсам из Ирака (конец - начало вв.) (основывался на предположении, что конец движущегося перпендикуляра к прямой описывает прямую линию),
иранский математики Омар Хайям (2-я половина - начало XII вв.) и Насир ад-Дин ат-Туси (XIII в.) (основывались на предположении, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения),
немецкий математик Клавиус (),
итальянские математики
- Катальди (впервые в 1603 году напечатал работу, целиком посвященную вопросу о параллельных),
английский математик Валлис ( , опубликовано в ) (основывался на предположении, что для всякой фигуры существует ей подобная, но не равная фигура),
французский математик Лежандр () (основывался на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла; у него также были другие попытки доказательства).

При этих попытках доказательства пятого постулата математики вводили некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

итальянский математик Саккери () (сформулировав противоречащее постулату утверждение, он вывел ряд следствий и, ошибочно признав часть из них противоречивыми, он счёл постулат доказанным),
немецкий математик Ламберт (около , опубликовано в ) (проведя исследования , он признал, что не смог обнаружить в построенной им системе противоречия).

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

немецкие математики Ф. Швейкарт () и Тауринус () (однако они не осознали, что такая теория будет логически столь же стройной).

Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи , а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отзывается о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории.

Хотя геометрия Лобачевского развивалась как умозрительная теория и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логической непротиворечивости.

Утверждение геометрии Лобачевского

угол - ещё сложнее.

Модель Пуанкаре

Содержание геометрии Лобачевского

Пучок параллельных прямых в геометрии Лобачевскоого

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют так называемую абсолютную геометрию , к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

Через точку P , не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x , y , которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности ) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а , а с другой - бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a) :

Здесь q - некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Сумма углов всякого треугольника меньше π и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность δ = π − (α + β + γ) , где α , β , γ - углы треугольника, пропорциональна его площади:

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: πq 2 .

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой , или гиперциклом .

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью , или орициклом .

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность - предельная сфера, или орисфера ; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число π не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от π ; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2π , и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Приложения

Сам Лобачевский применил свою геометрию к вычислению определённых интегралов .
В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций . Связь с геометрией Лобачевского была здесь отправным пунктом исследований Пуанкаре , который писал, что «неевклидова геометрия есть ключ к решению всей задачи».
Геометрия Лобачевского находит применение также в теории чисел , в её геометрических методах, объединённых под названием «геометрия чисел ».
Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности . Эта связь основана на том, что равенство, выражающее закон распространения света

при делении на t 2 , то есть для скорости света, даёт

- уравнение сферы в пространстве с координатами v x , v y , v z - составляющими скорости по осям х , у , z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с , то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

Замечательное приложение геометрия Лобачевского нашла в общей теории относительности . Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается возможным, что при определённых условиях пространство имеет геометрию Лобачевского. Таким образом, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.
При помощи модели Клейна, даётся очень простое и короткое доказательство

Геометрия Лобачевского (гиперболическая геометрия) - одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются. Геометрия Лобачевского имеет обширные применения, как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.

Модель планиметрии Лобачевского на евклидовой плоскости была построена французским математиком Анри Пуанкаре в 1882 г.

На евклидовой плоскости проведём горизонтальную прямую. Эта прямая называется абсолютом (x). Точки евклидовой плоскости, лежащие выше абсолюта, являются точками плоскости Лобачевского. Плоскостью Лобачевского называется открытая полуплоскость, лежащая выше абсолюта. Неевклидовы отрезки в модели Пуанкаре - это дуги окружностей с центром на абсолюте или отрезки прямых, перпендикулярных абсолюту (AB, CD). Фигура на плоскости Лобачевского - фигура открытой полуплоскости, лежащей выше абсолюта (F). Неевклидово движение является композицией конечного числа инверсий с центром на абсолюте и осевых симметрий, оси которых перпендикулярны абсолюту. Два неевклидовых отрезка равны, если один из них неевклидовым движением можно перевести в другой. Таковы основные понятия аксиоматики планиметрии Лобачевского.

Все аксиомы планиметрии Лобачевского непротиворечивы.

Определение прямой следующее: "Неевклидова прямая - это полуокружность с концами на абсолюте или луч с началом на абсолюте и перпендикулярный абсолюту". Таким образом, утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой a и точки A, не лежащей на этой прямой, но и для любой прямой a и любой не лежащей на ней точки A.

За геометрией Лобачевского возникли и другие непротиворечивые геометрии: от евклидовой отделилась проективная геометрия, сложилась многомерная евклидова геометрия, возникла риманова геометрия (общая теория пространств с произвольным законом измерения длин) и др. Из науки о фигурах в одном трёхмерном евклидовом пространстве геометрия за 40 - 50 лет превратилась в совокупность разнообразных теорий, лишь в чём-то сходных со своей прародительницей - геометрией Евклида.

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида - аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в "Началах" Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида. геометрия лобачевский евклидовый

Среди пытавшихся доказать были следующие учёные: древнегреческие математики Птолемей (II в.), Прокл (V в.) (основывался на предположении о конечности расстояния между двумя параллельными), Ибн аль-Хайсам из Ирака (конец X - начало XI вв.) (основывался на предположении, что конец движущегося перпендикуляра к прямой описывает прямую линию), иранские математики Омар Хайям (2-я половина XI - начало XII вв.) и Насир ад-Дин ат-Туси (XIII в.) (основывались на предположении, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения), немецкий математик Клавиус (1574), итальянские математики Катальди (впервые в 1603 году напечатал работу, целиком посвященную вопросу о параллельных), Борелли (1658), Дж. Витале (1680), английский математик Валлис (1663, опубликовано в 1693) (основывался на предположении, что для всякой фигуры существует ей подобная, но не равная фигура), французский математик Лежандр (1800) (основывался на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла; у него также были другие попытки доказательства).

При этих попытках доказательства пятого постулата математики вводили некоторое новое утверждение, казавшееся им более очевидным. Были предприняты попытки использовать доказательство от противного:

итальянский математик Саккери (1733) (сформулировав противоречащее постулату утверждение, он вывел ряд следствий и, ошибочно признав часть из них противоречивыми, он счёл постулат доказанным),

немецкие математики Швейкарт (1818) и Тауринус (1825) (однако они не осознали, что такая теория будет логически столь же стройной).

Лобачевский в работе "О началах геометрии" (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г.Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее "воображаемой геометрией"; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории. Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её "воображаемой геометрией", тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логической непротиворечивости.

Лобачевский строил свою геометрию , отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько аксиом геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол и между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой - бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a):

Сумма углов всякого треугольника меньше р и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность

д = р? (б + в + г),

где б, в, г - углы треугольника, пропорциональна его площади:

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: рq2.

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность - предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число р не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от р; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2р, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле "предельный" случай геометрии Лобачевского.

Лобачевского геометрия - геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Лобачевского геометрия вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Лобачевского геометрия имеет вполне реальный смысл. Лобачевского геометрия была создана и развита Н. И. Лобачевским, который впервые сообщил о ней в 1826. Лобачевского геометрия называется неевклидовой геометрией, хотя обычно термину «неевклидова геометрия» придают более широкий смысл, включая сюда и др. теории, возникшие вслед за Лобачевского геометрия и также основанные на изменении основных посылок евклидовой геометрии. Лобачевского геометрия называется специально гиперболической неевклидовой геометрией (в противоположность эллиптической геометрии Римана).

Лобачевского геометрия представляет теорию, богатую содержанием и имеющую применение как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще (см. Геометрия). С современной точки зрения можно дать, например, следующее определение Лобачевского геометрия на плоскости: она есть не что иное, как геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым образом. Именно, будем рассматривать круг на обычной плоскости (рис. 1) и внутренность его, т. е. круг, за исключением ограничивающей его окружности, назовем «плоскостью». Точкой «плоскости» будет точка внутри круга. «Прямой» будем называть любую хорду (например, а, b, b`, MN) (с исключенными концами, т. к. окружность круга исключена из «плоскости»). «Движением» назовем любое преобразование круга самого в себя, которое переводит хорды в хорды.

Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому Лобачевского геометрия Иными словами, всякое утверждение Лобачевского геометрия на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, т. к. через точку О, не лежащую на данной хорде а (т. е. «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b`). Аналогично, Лобачевского геометрия в пространстве может быть определена как геометрия внутри шара, выраженная в соответствующих терминах («прямые» - хорды, «плоскости» - плоские сечения внутренности шара, «равные» фигуры - те, которые переводятся одна в другую преобразованиями, переводящими шар сам в себя и хорды в хорды). Таким образом, Лобачевского геометрия имеет совершенно реальный смысл и столь же непротиворечива, как геометрия Евклида. Описание одних и тех же фактов в разных терминах или, напротив, описание разных фактов в одних и тех же терминах представляет характерную черту математики. Она ясно выступает, например, когда одна и та же линия задаётся в разных координатах разными уравнениями или, напротив, одно и то же уравнение в разных координатах представляет различные линии.

Возникновение геометрии Лобачевского

Источником Лобачевского геометрия послужил вопрос об аксиоме о параллельных, которая известна также как V постулат Евклида (под этим номером утверждение, эквивалентное приведённой выше аксиоме о параллельных, фигурирует в списке постулатов в «Началах» Евклида). Этот постулат, ввиду его сложности в сравнении с другими, вызвал попытки дать его доказательство на основании остальных постулатов.

Вот неполный перечень учёных, занимавшихся доказательством V постулата до 19 в.: древнегреческий математики Птолемей (2 в.), Прокл (5 в.) (доказательство Прокла основано на предположении о конечности расстояния между двумя параллельными), Ибн аль-Хайсам из Ирака (конец 10 - начало 11 вв.) (Ибн аль-Хайсам пытался доказать V постулат, исходя из предположения, что конец движущегося перпендикуляра к прямой описывает прямую линию), таджикский математик Омар Хайям (2-я половина 11 - начало 12 вв.), азербайджанский математик Насирэддин Туей (13 в.) (Хайям и Насирэддин при доказательстве V постулата исходили из предположения, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения), немецкий математик К. Клавий (Шлюссель, 1574), итальянские математики П. Катальди (впервые в 1603 напечатавший работу, целиком посвященную вопросу о параллельных), Дж. Борелли (1658), Дж. Витале (1680), английский математик Дж. Валлис (1663, опубликовано в 1693) (Валлис основывает доказательство V постулата на предположении, что для всякой фигуры существует ей подобная, но не равная фигура). Доказательства перечисленных выше геометров сводились к замене V постулата др. предположением, казавшимся более очевидным.

Итальянский математик Дж. Саккери (1733) сделал попытку доказать V постулат от противного. Приняв предложение, противоречащее постулату Евклида, Саккери развил из него довольно обширные следствия. Ошибочно признав некоторые из этих следствий приводящими к противоречиям, Саккери заключил, что постулат Евклида доказан. Немецкий математик И. Ламберт (около 1766, опубликовано в 1786) предпринял аналогичные исследования, однако он не повторил ошибки Саккери, а признал своё бессилие обнаружить в построенной им системе логическое противоречие. Попытки доказательства постулата предпринимались и в 19 в. Здесь следует отметить работы французского математика А. Лежандра; одно из его доказательств (1800) основано на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла, т. е., как и все его предшественники, он заменил постулат др. допущением. Довольно близко к построению Лобачевского геометрия подошли немецкие математики Ф. Швейкарт (1818) и Ф. Тауринус (1825), однако ясно выраженной мысли о том, что намечаемая ими теория будет логически столь же совершенна, как и геометрия Евклида, они не имели.

Вопрос о V постулате Евклида, занимавший геометров более двух тысячелетий, был решен Лобачевским. Это решение сводится к тому, что постулат не может быть доказан на основе др. посылок евклидовой геометрии и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий. Лобачевский сделал об этом сообщение в 1826, а в 1829-30 напечатал работу «О началах геометрии» с изложением своей теории. В 1832 была опубликована работа венгерского математика Я. Больяй аналогичного содержания. Как выяснилось впоследствии, немецкий математик К. Ф. Гаусс также пришёл к мысли о возможности существования непротиворечивой неевклидовой геометрии, но скрывал её, опасаясь быть непонятым. Хотя Лобачевского геометрия развивалась как умозрительная теория и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решен вопрос о её реальном смысле, логической непротиворечивости.

Лобачевского геометрия изучает свойства «плоскости Лобачевского» (в планиметрии) и «пространства Лобачевского» (в стереометрии). Плоскость Лобачевского - это плоскость (множество точек), в которой определены прямые линии, а также движения фигур (вместе с тем - расстояния, углы и пр.), подчиняющиеся всем аксиомам евклидовой геометрии, за исключением аксиомы о параллельных, которая заменяется указанной выше аксиомой Лобачевского. Сходным образом определяется пространство Лобачевского. Задача выяснения реального смысла Лобачевского геометрия состояла в нахождении моделей плоскости и пространства Лобачевского, т. е. в нахождении таких объектов, в которых реализовались бы соответствующим образом истолкованные положения планиметрии и стереометрии Лобачевского геометрии.

Приведём несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским

1) В Лобачевского геометрия не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, например, сторона правильного треугольника с данной суммой углов.

2) Сумма углов всякого треугольника меньше p и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность p - (a + b + g), где a, b, g - углы треугольника, пропорциональна его площади.

3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих а и находящихся с ней в одной плоскости; среди них есть две крайние b, b`, которые и называются параллельными прямой а в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) а общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек) (рис. 1,3). Угол ее между прямой b (или b`) и перпендикуляром из О на а - т. н. угол параллельности - по мере удаления точки О от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель b с одной стороны (а b` с противоположной) асимптотически приближается к а, а с другой - бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

5) Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

6) Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность - предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

8) Длина окружности не пропорциональна радиусу, а растет быстрее.

9) Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от p; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2p, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы Лобачевского геометрия переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай Лобачевского геометрии.

Лобачевского геометрия продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. Ряд геометров развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрическим идеям. В целом Лобачевского геометрия является обширной областью исследования, подобно геометрии Евклида.

Геометрия Лобачевского

(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются . Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой , что знаменовало новую эпоху в развитии геометрии , математики и науки вообще.

История

Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида - аксиома, эквивалентная аксиоме о параллельных . Он входил в список постулатов в «Началах» Евклида . Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

итальянский математик Саккери () (сформулировав противоречащее постулату утверждение, он вывел ряд следствий и, ошибочно признав часть из них противоречивыми, он счёл постулат доказанным),
немецкий математик Ламберт (около , опубликовано в ) (проведя исследования , он признал, что не смог обнаружить в построенной им системе противоречия).

немецкие математики Швейкарт () и Тауринус () (однако они не осознали, что такая теория будет логически столь же стройной).

Создание неевклидовой геометрии

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи , а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии. Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно он впервые открыто предложил её не как игру ума, а как возможную и полезную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации (модели).

Утверждение геометрии Лобачевского

Модель Пуанкаре

Содержание геометрии Лобачевского

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию , к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Сумма углов всякого треугольника меньше и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность , где , , - углы треугольника, пропорциональна его площади:

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: .

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от ; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от , и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Заполнение плоскости и пространства правильными политопами

Замощение плоскости Лобачевского правильными треугольниками ({3;7})

Плоскость Лобачевского может быть замощена не только правильными треугольниками , квадратами и шестиугольниками , но и любыми другими правильными многоугольниками . При этом в одной вершине паркета должно сходиться не менее 7 треугольников, 5 квадратов, 4 пяти- и шестиугольников и 3 многоугольников с числом сторон более 6. Каждое замощение (в одной вершине сходится M N-угольников) требует строго определённого размера единичного N-угольника, в частности, его площадь должна равняться:

Заполнение пространства Лобачевского правильными додекаэдрами ({5,3,4})

В отличие от обычного пространства, которое можно заполнить правильными многогранниками только одним способом (по 8 кубов в вершине), трёхмерное пространство Лобачевского можно заполнить правильными многогранниками четырьмя способами:

{3,5,3} (по 12 икосаэдров в вершине)
{4,3,5} (по 20 кубов в вершине)
{5,3,4} (по 8 додекаэдров в вершине)
{3,5,3} (по 20 додекаэдров в вершине)

Кроме этого, существует 11 способов заполнить пространство Лобачевского правильными мозаичными орисферами.

Приложения

Сам Лобачевский применил свою геометрию к вычислению определённых интегралов .
В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций . Связь с геометрией Лобачевского была здесь отправным пунктом исследований Пуанкаре , который писал, что «неевклидова геометрия есть ключ к решению всей задачи».
Геометрия Лобачевского находит применение также в теории чисел , в её геометрических методах, объединённых под названием «геометрия чисел ».
Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности . Эта связь основана на том, что равенство, выражающее закон распространения света

при делении на , то есть для скорости света, даёт - уравнение сферы в пространстве с координатами , , - составляющими скорости по осям х , у , z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с , то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

Замечательное приложение геометрия Лобачевского нашла в общей теории относительности . Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается возможным, что при определённых условиях пространство имеет геометрию Лобачевского. Таким образом, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.
При помощи модели Клейна, даётся очень простое и короткое доказательство теоремы о бабочке в евклидовой геометрии.

См. также

Примечания

Труды основоположников

Н. И. Лобачевский «Геометрические исследования по теории параллельных линий» . - 1941.
Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию ее идей. М.: Гостехиздат, 1956.

Литература

Александров А. Д., Нецветаев Н. Ю. Геометрия, - Наука, Москва, 1990.
Александров П. С. Что такое неэвклидова геометрия, - УРСС, Москва, 2007.
Делоне Б. Н. Элементарное доказательство непротиворечивости планиметрии Лобачевского, - Гостехиздат, Москва, 1956.
Иовлев Н. Н. «Введение в элементарную геометрию и тригонометрию Лобачевского» . - М.-Л.: Гиз., 1930. - С. 67.
Клейн Ф. «Неевклидова геометрия» . - М.-Л.: ОНТИ, 1936. - С. 356.
Попов А. Г.

Пятый постулат Евклида «Если прямая, падающая на две прямые, образует внутренние односторонние углы, в сумме меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы в сумме меньше двух прямых» многим математикам еще в античности казался каким-то не очень ясным, отчасти в связи со сложностью его формулировки.

Представлялось, что постулатами должны быть только элементарные предложения, простые по форме. В связи с этим 5-ый постулат стал предметом особого внимания математиков, причем исследования на эту тему можно разделить на два направления, на деле тесно связанные между собой. Первое стремилось к замене этого постулата более простым и интуитивно ясным, как, например, сформулированное еще Проклом утверждение «Через точку, не лежащую на данной прямой, можно провести только одну прямую, не пересекающуюся с данной»: именно в таком виде 5-ый постулат, вернее, эквивалентная ему аксиома о параллельных фигурирует в современных учебниках.

Представители второго направления пытались доказать пятый постулат на основе других, то есть превратить его в теорему. Попытки такого рода начали ряд арабских математиков средневековья: ал-Аббас ал-Джаухари (нач. IX в.), Сабит ибн Корра, Ибн ал-Хайсам, Омар Хайям, Насиреддин ат-Туси. Позже в эти исследования включились европейцы: писавшие по-древнееврейски Леви Бен Гершон (XIV в.) и Альфонсо (XV в.), а затем немец-иезуит Х. Клавий (1596), англичанин Дж. Валлис (1663) и др. Особенный интерес к этой проблеме возник в XVIII в.: с 1759 по 1800 г. вышло 55 сочинений, анализирующих данную проблему, в т. ч. весьма важные сочинения итальянца-иезуита Дж. Саккери и немца И. Г. Ламберта.

Доказательства обычно велись методом «от противного»: из допущения, что 5-ый постулат не выполняется, пытались вывести следствия, которые противоречили бы другим постулатам и аксиомам. В действительности, однако, в конечном итоге получали противоречие не с другими постулатами, а с неким явным или неявным «очевидным» предложением, которое, однако, было невозможно установить на основе других постулатов и аксиом евклидовой геометрии: таким образом, доказательства не достигали своей цели, – получалось, что на место 5-го постулата опять-таки ставилось какое-то другое равносильное ему утверждение. В качестве такого утверждения брались, например, следующие положения:

Рис. 2. Существуют прямые, равноотстоящие друг от друга

Рис. 4. Две сходящиеся прямые пересекаются

Геометрия, в которой эти утверждения не выполняются, конечно, не такова, как мы привыкли, но из этого еще не следует, что она невозможна или что эти утверждения вытекают из других постулатов и аксиом Евклида, так что во всех доказательствах были те или иные пробелы или натяжки. Клавий обосновывал допущение о том, что существуют прямые, равноотстоящие друг от друга, евклидовым «определением» прямой как линии, равно расположенной по отношению к точкам на ней. Валлис впервые положил в основание своего доказательства 5-го постулата «естественное» положение, согласно которому для любой фигуры существует подобная сколь угодно большого размера, и обосновывал это утверждение 3-м постулатом Евклида, утверждающим из всякого центра и всяким раствором может быть описан круг (в действительности утверждение о существовании, например, неравных подобных треугольников или даже окружностей эквивалентно 5-му постулату). А. М. Лежандр в последовательных изданиях учебника «Начала геометрии» (1794, 1800, 1823) приводил новые доказательства 5-го постулата, но внимательный анализ показывал пробелы в этих доказательствах. Подвергнув Лежандра справедливой критике, наш соотечественник С. Е. Гурьев в книге «Опыт о усовершенствовании элементов геометрии» (1798), однако, сам допустил ошибку в доказательстве 5-го постулата.

Довольно быстро была осознана связь между суммой углов треугольника и четырехугольника и 5-ым постулатом: 5-ый постулат следует из утверждения о том, что сумма углов треугольника равна двум прямым, которое можно вывести из существования прямоугольников. В связи с этим получил распространение подход (ему следовали Хайям, ат-Туси, Валлис, Саккери), при котором рассматривается четырехугольник, получающийся в результате откладывания равных отрезков на двух перпендикулярах к одной прямой. Исследуются три гипотезы: два верхних угла являются острыми, тупыми либо прямыми; при этом осуществляется попытка показать, что гипотезы тупых и острых углов ведут к противоречию.

При другом подходе (его применяли Ибн ал-Хайсам, Ламберт) анализировались аналогичные три гипотезы для четырехугольника с тремя прямыми углами.

Саккери и Ламберт показали, что гипотезы тупых углов действительно ведут к противоречию, но им не удалось найти противоречия при рассмотрении гипотез острых углов: вывод о таком противоречии Саккери сделал лишь в результате ошибки, а Ламберт заключил, что видимое отсутствие противоречия в гипотезе острого угла связано с какой-то фундаментальной причиной. Ламберт нашел, что, при принятии гипотезы острого угла, сумма углов каждого треугольника меньше 180° на величину, пропорциональную его площади, и сравнил с этим открытое в нач. XVII в. положение, согласно которому площадь сферического треугольника, напротив, больше 180° на величину, пропорциональную его площади.

В 1763 г. Г. С. Клюгель опубликовал «Обзор важнейших попыток доказательства теории параллельных линий», где рассмотрел около 30 доказательств 5-го постулата и выявил в них ошибки. Клюгель заключил, что Евклид вполне обосновано поместил свое утверждение среди постулатов.

Тем не менее, попытки доказательства 5-го постулата сыграли весьма важную роль: пытаясь привести противоположные ему утверждения к противоречию, указанные исследователи на деле открыли многие важные теоремы неевклидовой геометрии – в частности, такой геометрии, где место 5-го постулата занимает утверждение о возможности провести через заданную точку, по крайней мере, двух прямых, не пересекающих данную. Это утверждение, эквивалентное гипотезе острого угла, и было положено в основу первооткрывателями неевклидовой геометрии.

К мысли о том, что допущение альтернативы 5-му постулату ведет к построению геометрии, отличной от евклидовой, но столь же непротиворечивой, независимо пришли несколько ученых: К. Ф. Гаусс, Н. И. Лобачевский и Я. Бояи (а также Ф. К. Швейкарт и Ф. А. Тауринус, чей вклад в новую геометрию, впрочем, был более скромным и которые не публиковали своих исследований). Гаусс, судя по записям, сохранившимся в его архиве (и опубликованным только в 1860-е гг.), осознал возможность новой геометрии еще в 1810-е гг., но также никогда не публиковал своих открытий на эту тему: «Я опасаюсь крика беотийцев (т. е. глупцов: жители области Беотия считались в Древней Греции самыми глупыми), если выскажу мои воззрения целиком», – писал он в 1829 г. своему другу математику Ф. В. Бесселю. Непонимание в полной мере выпало на долю Лобачевского, сделавшего первый доклад о новой геометрии в 1826 г. и опубликовавшего полученные результаты в 1829 г. В 1842 г. Гаусс добился избрания Лобачевского членом-корреспондентом Геттингенского ученого общества: это было единственным признанием заслуг Лобачевского при жизни. Отец Я. Бояи – математик Фаркаш Бояи, также пытавшийся доказать 5-й постулат – предостерегал сына от исследований в этом направлении: «...это может лишить тебя твоего досуга, здоровья, покоя, всех радостей жизни. Эта черная пропасть в состоянии, быть может, поглотить тысячу таких титанов, как Ньютон, на Земле это никогда не прояснится...». Тем не менее, Я. Бояи в 1832 г. опубликовал свои результаты в приложении к учебнику геометрии, написанному его отцом. Бояи также не добился признания, к тому же был огорчен тем, что Лобачевский опередил его: больше неевклидовой геометрией он не занимался. Так что только Лобачевский в течение всей оставшейся жизни, во-первых, продолжал исследования в новой области, а во-вторых, пропагандировал свои идеи, опубликовал еще ряд книг и статей по новой геометрии.

Итак, в плоскости Лобачевского через точку C вне данной прямой AB проходят по крайней мере две прямые, не пересекающие AB . Все прямые, проходящие через C , делятся на два класса – на пересекающие и на не пересекающие AB . Эти последние лежат в некотором угле, образованном двумя крайними прямыми, не пересекающими AB . Именно эти прямые Лобачевский называет параллельными прямой AB , а угол между ними и перпендикуляром – углом параллельности. Этот угол зависит от расстояния от точки C до прямой AB : чем больше это расстояние, тем меньше угол параллельности. Прямые, лежащие внутри угла, называются расходящимися по отношению к AB .

Любые две расходящиеся прямые p и q имеют единственный общий перпендикуляр t , который является самым коротким отрезкам от одной до другой. Если точка M движется по p в направлении от t , то расстояние от M до q будет возрастать до бесконечности, причем основания перпендикуляров, опущенных из M на q , заполнят лишь конечный отрезок.

Если прямые p и q пересекают друг друга, то проекции точек одной из них на другую также заполняют ограниченный отрезок.

Если прямые p и q параллельны, то в одном направлении расстояния между их точками неограниченно убывают, а в другом неограниченно возрастают; одна прямая проецируется на луч другой.

На рисунках показаны различные взаимные положения прямых p и q , возможные в геометрии Лобачевского; r и s – перпендикуляры, параллельные q . (Мы вынуждены рисовать искривленную линию q , хотя речь идет о прямой. Даже если бы наш мир в целом подчинялся бы законам геометрии Лобачевского, мы бы все равно не смогли изобразить в малом масштабе без искажений то, как все выглядит в большом: в геометрии Лобачевского нет подобных фигур, которые не были бы равными).

Внутри угла существует прямая, параллельная обеим сторонам угла. Она делит все точки внутри угла на два типа: через точки первого типа можно провести прямые, пересекающие обе стороны угла; через точки второго типа нельзя провести ни одной такой прямой. То же верно и для пространства между параллельными прямыми. Между двумя расходящимися прямыми есть две прямые, параллельные им обеим; они делят пространство между расходящимися прямыми на три области: через точки в одной области можно провести прямые, пересекающие обе стороны угла; через точки в двух других областях таких прямых провести нельзя.

На диаметр окружности всегда опирается острый, а не прямой угол. Сторона вписанного в окружность правильного шестиугольника всегда больше ее радиуса. Для любого n > 6 можно построить такую окружность, что сторона вписанного в нее правильного n -угольника равна ее радиусу.

Лобачевский интересовался вопросом о геометрии физического пространства, в частности, используя данные астрономических наблюдений подсчитывал сумму углов больших, межзвездных треугольников: однако отличие этой суммы углов от 180° лежало целиком внутри ошибки наблюдений. Непонимание, выпавшее на долю Лобачевского, который сам называл свою геометрию «воображаемой», во многом связано с тем, что в его время такие идеи казались чистыми абстракциями и игрой воображения. Действительно ли новая геометрия непротиворечива? (Ведь если даже Лобачевскому не удалось встретить противоречия, это не гарантирует, что оно не будет обнаружено впоследствии). Насколько она соотносится с реальным миром, а также с другими областями математики? Это стало ясно далеко не сразу, и успех, в конечном итоге выпавший на долю новых идей, был связан с открытием моделей новой геометрии.