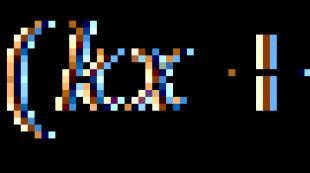Интегрирование степенных рядов. Степенные ряды. Теорема Абеля, радиус и интервал сходимости. Непрерывность суммы степенного ряда. Дифференцирование и интегрирование степенного ряда. Вопросы для самопроверки
СТЕПЕННЫЕ РЯДЫ Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Равномерная сходимость степенного ряда и непрерывность его суммы Интегрирование степенных рядов Дифференцирование степенных рядов Ряд Тейлора Условия разложимости функции в ряд Тейлора элементарных функций Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций.



















Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Степенным рядом называется функциональный ряд вида (о или вида (2) где коэффициенты. - постоянные. Ряд (2) формальной заменой х - х<> на х сводится к ряду (1). Степенной ряд (1) всегда сходится в точке х = 0, а ряд (2) - в точке х0, и их сумма в этих точках равна со. Пример. Ряды являются стеленными рядами. Выясним вид области сходимости степенного ряда. Теорема 1 (Абель). Если степенной ряд сходится при, то он сходится абсолютно для всех х таких, что если степенной ряд расходится при х = xi, то он расходится при любом х, для которого Пусть степенной ряд СХОДИТСЯ При. сходится числовой ряд СТЕПЕННЫЕ РЯДЫ Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Равномерная сходимость степенного ряда и непрерывность его суммы Интегрирование степенных рядов Дифференцирование степенных рядов Ряд Тейлора Условия разложимости функции в ряд Тейлора элементарных функций Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций. Отсюда следует, что а значит, существует число такое, что М для всех п. Рассмотрим ряд где и оценим его общий член. Имеем гдед= . Но ряд составлен из членов геометрической прогрессии со знаменателем q, где значит, сходится. На основании признака сравнения ряд 2 |с„:гп| сходится в любой точке х, для которой. Следовательно, степенной ряд абсолютно сходится ДЛЯ Пусть теперь степенной ряд точки О), которые отделяют интервалы расходимости от интервала сходимости. Имеет место следующая теорема. Теорема 2. Пусть степенной ряд сходится в точке х Ф 0. Тогда либо этот ряд абсолютно сходится в каждой точке числовой прямой, либо существует число R > О такое, что ряд сходится абсолютно при и расходится при Расходится. Абс. сходитсяРасходится д Рис. 1 Определение. Интервалом сходимости степенного ряда называется интервал (-R, Я), где R > 0, такой, что в каждой точке х € (-Д, R) ряд абсолютно сходится, а в точках х таких, что |я| > R, ряд расходится. Число R называется радиусом сходимости степенного ряда. Замечание. Что касается концов интервала сходимости (-R, Я), то возможны следующие три случая: I) степенной ряд сходится как в точке х = -R, так и в точке х = R, 2) степенной ряд расходится в обеих точках, 3) степенной ряд сходится в одном конце интервала сходимости и расходится в другом. Замечание. Степенной ряд где хо ф 0, имеет тот же радиус сходимости, что и ряд Для доказательства формулы (3) рассмотрим ряд, составленный из абсолютных величин членов данного ряда Применяя к этому ряду признак Даламбера, находим Отсюда следует, что ряд (4) будет сходиться, если и расходиться, если. степенной ряд сходится абсолютно для всех х таких, что и расходится при. По определению радиуса сходимости получаем, что Радиус сходимости степенного ряда можно находить также по формуле если существует конечный предел Формулу (5) легко получить, используя признак Коши. Если степенной ряд сходится только в точке х = 0, то говорят, что его радиус сходимости R = 0 (это возможно, например, при lim Ь^Д = оо или Если степенной ряд сходится во всех точках числовой оси, то полагают R = +оо (это имеет место, например, при lim п^р = 0 или Областью сходимости степенного ряда может оказаться либо интервал (, либо отрезок [, либо один из полуинтервалов (ж0 - R,x0 + Д) или [. Если R = +оо, то областью сходимости ряда будет вся числовая ось, т. е. интервал (-оо, +оо). Для отыскания области сходимости степенного ряда нужно сначала вычислить его радиус сходимости R (например, по одной из приведенных выше формул) и тем самым найти интервал сходимости точки О), которые отделяют интервалы расходимости от интервала сходимости. Имеет место следующая теорема. Теорема 2. Пусть степенной ряд сходится в точке х Ф 0. Тогда либо этот ряд абсолютно сходится в каждой точке числовой прямой, либо существует число R > О такое, что ряд сходится абсолютно при и расходится при | Расходится. Абс. сходится Расходится Определение. Интервалом сходимости степенного ряда называется интервал (-R, Я), где R > 0, такой, что в каждой точке х € (-Д, R) ряд абсолютно сходится, а в точках х таких, что |я| > R, ряд расходится. Число R называется радиусом сходимости степенного ряда. Замечание. Что касается концов интервала сходимости (-R, Я), то возможны следующие три случая: I) степенной ряд сходится как в точке х = -R, так и в точке х = R, 2) степенной ряд расходится в обеих точках, 3) степенной ряд сходится в одном конце интервала сходимости и расходится в другом. Замечание. Степенной ряд где хо ф 0, имеет тот же радиус сходимости, что и ряд Для доказательства формулы (3) рассмотрим ряд, составленный из абсолютных величин членов данного ряда Применяя к этому ряду признак Даламбера, находим Отсюда следует, что ряд (4) будет сходиться, если \, и расходиться, если, т. е. степенной ряд сходится абсолютно для всех х таких, что и расходится при \. По определению радиуса сходимости получаем, что R = £, т. е. СТЕПЕННЫЕ РЯДЫ Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Равномерная сходимость степенного ряда и непрерывность его суммы Интегрирование степенных рядов Дифференцирование степенных рядов Ряд Тейлора Условия разложимости функции в ряд Тейлора элементарных функций Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций. Радиус сходимости степенного ряда можно находить также по формуле если существует конечный предел Формулу (5) легко получить, используя признак Коши. Если степенной ряд сходится только в точке х = 0, то говорят, что его радиус сходимости R = 0 (это возможно, например, при lim Ь^Д = оо или. Если степенной ряд сходится во всех точках числовой оси, то полагают R = +оо (это имеет место, например, при Областью сходимости степенного ряда может оказаться либо интервал (, либо отрезок ], либо один из полуинтервалов (ж0 - R,x0 + Д) или [. Если R = +оо, то областью сходимости ряда будет вся числовая ось, т. е. интервал (-оо, +оо). Для отыскания области сходимости степенного ряда нужно сначала вычислить его радиус сходимости R (например, по одной из приведенных выше формул) и тем самым найти интервал сходимости в котором ряд абсолютно сходится, затем - исследовать.сходимость ряда в.концах интервала сходимости - в точках х = хо - R, х = xq + R. Пример 1. Найти область сходимости степенного ряда М 1) Для нахождения радиуса сходимости R данного ряда удобно применить формулу (3). Так както будем иметь Ряд сходится абсолютно на интервале 2) Исследуем сходимость ряда (6) в концах интервала сходимости. Положив х = -1, получим числовой ряд расходимость которого очевидна (не выполнен необходимый признак сходимости: . При х - 1 получим числовой ряд для которого не существует, а значит, этот ряд расходится. Итак, область сходимости ряда (6) есть интервал Пример 2. Найти область сходимости ряда М 1) Радиус сходимости находим по формуле (3). Имеем Ряд (7) сходится абсолютно на интервале, откуда При получим числовой ряд который расходится (гармонический ряд). При х = 0 будем иметь числовой ряд сходящийся условно. Таким образом, ряд (7) сходится в области Пример 3. Найти интервал сходимости ряда Так как = , то для нахождения радиуса сходимости применим формулу Это означает, что данный ряд сходится при всех значениях х, т.е. областью сходимости является интервал Пример 4. Найти интервал сходимости ряда, то получим Равенство R = 0 означает, что ряд (8) сходится только в точке. е. область сходимости данного степенного ряда состоит из одной точки §2. Равномерная сходимость степенного ряда и непрерывность его суммы Теорема 1. Степенной ряд сходится абсолютно и равномерно на любом отрезке, содержащемся в интервале сходимости ряда Пусть. Тогда для всех ж, удовлетворяющих условию, и для любого п =. будем иметь. Но так как числовой ряд сходится, то по признаку Вейерштрасса данный степенной ряд сходится на отрезке абсолютно и равномерно. Теорема 2. Сумма степенного ряда непрерывна в каждой точке ж его интервала сходимости (4 Любую точку ж из интервала сходимости (-Д, R) можно заключить в некоторый отрезок, на котором данный ряд сходится равномерно. Так как члены ряда непрерывны, то его сумма S(x) будет непрерывной на отрезке [-а, а], а значит, и в точке х. Интегрирование степенных рядов Теорема 3 (о почленном интегрировании степенного ряда). Степенной ряд можно интегрировать почленно в его интервале сходимости (-R, R), R > О, причем радиус сходимости ряда, полученного почленным интегрированием, также равен R. В частности, для любого х из интервала (-R, R) справедлива формула Любую точку х из интервала сходимости (-Д, R) можно заключить в некоторый отрезок [-а, а], где. На этом отрезке данный ряд будет сходиться равномерно, а так как члены ряда непрерывны, то его можно почленно интегрировать, например, в пределах от 0 до ж. Тогда, согласно теореме 4 главы XVIII, Найдем радиус сходимости R" полученного ряда СТЕПЕННЫЕ РЯДЫ Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Равномерная сходимость степенного ряда и непрерывность его суммы Интегрирование степенных рядов Дифференцирование степенных рядов Ряд Тейлора Условия разложимости функции в ряд Тейлора элементарных функций Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций. при дополнительном условии существования конечного предела R. Име Итак, радиус сходимости степенного ряда при интегрировании не меняется. Замечание. Утверждение теоремы остается справедливым и при Я = +оо. §4. Дифференцирование степенных рядов Теорема 4 (о почленном дифференцировании степенного ряда). Степенной ряд можно дифференцировать почленно в любой точке х его интервала сходимости 4 Пусть R - радиус сходимости ряда a R" - радиус сходимости ряда Предположим, что существует (конечный или бесконечный) предел Найдем радиус В! ряда где Имеем Тем самым, радиусы сходимости рядов (1) и (2) равны. Обозначим сумму ряда (2) через Ряды (1) и (2) равномерно сходятся на любом отрезке [-а, а|, где. При этом все члены ряда (2) непрерывны и являются производными соответствующих членов ряда (1). Поэтому, согласно теореме 5 главы XVIII, на отрезке [-а, а) выполняется равенство. В силу произвольности а последнее равенство выполнено и на интервале Следспие. Степенной ряд Определение. Будем говорить, что функция /(ж) разлагается в степенной ряд ]Г) СпХп на интервале, если на этом интервале указанный ряд сходится и его сумма равна /(ж): Докажем сначала, что функция /(ж) не может иметь двух различных разложений в степенной ряд вида Теорема 5. Если функция /(ж) на интервале (-R, R) разлагается в степенной ряд (1), то это разложение единственно, т. е. коэффициенты ряда (1) по его сумме определяются однозначно. Пусть функция в интервале разложена в сходящийся степенной ряд Дифференцируя этот ряд почленно п раз, найдем При ж = 0 получаем откуда Таким образом, коэффициенты степенного ряда (1) формулой (2) определяются однозначно. Замечание. Если функция /(х) разложена в степенной ряд по степеням разности x-zq, то коэффициенты с„ этого ряда определяются формулами. Пусть функция / имеет производные всех порядков.е. является бесконечно дифференцируемой в точке жо. Составим дня этой функции формальный степенной ряд вычислив его коэффициенты по формуле (3). §5. Определение. Рядом Тейлора функции /(х) относительно точки х0 называется степенной ряд вида (здесь. Коэффициенты этого ряда.. называются коэффициентами Тейлора функции. При хо = 0 ряд Тейлора называют рядом Маклорена. Из теоремы 5 вытекает следующее утверждение. Теорема б. Если на интервале функция /(х) разлагается в степенной ряд то этот ряд является рядом Тейлора функции /(х). Пример 1. Рассмотрим функцию и найдем ее производные. Для z О эта функция имеет производные всех порядков, которые находятся по обычным правилам и, вообще, где Pjn (i) - многочлен степени 3п относительно j. Покажем теперь, что в точке 2 = 0 данная функция также имеет производные любого порядка, причем все они равны нулю. Исходя из определения производной, имеем (при вычислении предела мы применили правило Яопиталя). Аналогичным образом можно доказать, что Тем самым, заданная функция имеет на числовой оси производные всех порядков. Построим формальный ряд Тейлора исходной функции относительно точки z0 = Имеем. Очевидно, что сумма этого ряда тождественно равна нулю, в то время как сама функция f(x) тождественно равной нулю не является. ^ Про этот пример стоит вспомнить при обсуждении комплексного анализа (аналитичности): функция, внешне совершенно благопристойная, проявляет на действительной оси капризный характер, являющийся следствием неприятностей на мнимой оси. Формально построенный в примере для заданной бесконечно дифференцируемой функции ряд сходится, но его сумма не совпадает со значениями этой функции при х Ф 0. В связи с этим возникает естественный вопрос: каким условиям должна удовлетворять функция f(x) на интервале (жо - R,xo + R), чтобы ее можно было разложить в сходящийся к ней ряд Тейлора? Условия разложимости функции в ряд Тейлора Для простоты будем рассматривать степенной ряд вида т. е. ряд Маклорена. Теорема 7. Для того чтобы функцию f(x) можно было разложить в степенной ряд на интервале (-R, R), необходимо и достаточно, чтобы на этом интервале функция f(x) имела производные всех порядков и чтобы в ее формуле Тейлора остаточный член Rn(x) стремился к нулю при для всех м Необходимость. Пусть на интервале (функция f(x) разложима в степенной ряд т. е. ряд (2) сходится и его сумма равна f(x). Тогда по теореме 4 и следствию из нее функция f(x) имеет на интервале (-R, R) производные /(п^(х) всех порядков. По теореме 5 (формула (2)) коэффициенты ряда (2) имеют вид т. е. мы можем написать равенство В силу сходимости этого ряда на интервале (-R, R) его остаток 0 стремится к нулю при п оо для всех х Достаточность. Пусть функция /(яг) на интервале (-R, R) имеет производные всех порядков и в ее формуле Тейлора остаточный член Rn(x) 0 при п оо для любого х € (-Д, R). Поскольку при п -» оо. Поскольку в квадратных скобках записана n-я частичная сумма ряда Тейлора, то формула (4) означает, что ряд Тейлора функции f(x) сходится на интервале (-Д, R) и его суммой является функция f(x). Достаточные условия разложимости функции в степенной ряд, удобные для практического применения, описываются следующей теоремой. Теорема 8. Для того, чтобы функцию f(x) на интервале {-R, R) можно было разложить в степенной ряд достаточно, чтобы функция f(x) имела на этом интервале производные всех порядков и чтобы существовала постоянная М > О такая, что. Пусть функция f(x) имеет на интервале (-Д, R) производные всех порядков. Тогда для нее можно формально написать ряд Тейлора Докажем, что он сходится к функции f(x). Для этого достаточно показать, что остаточный член в формуле Тейлора (1) стремится к нулю при п оо для всех х € (-Д, R). В самом деле, учитывая, что). Числовой ряд сходится в силу признака Даламбера: в силу необходимого признака сходимости. Из неравенства (3) получаем!отя функция янной М, от § б. Ряды Тейлора элементарных функций Рассмотрим разложения в ряд основных элементарных функций. 6 Эта функция имеет производные всех порядков на интервале (- любое число, причем Следовательно, показательная функция ех разлагается в ряд Тейлора на любом интервале (-а, а) и, тем самым, на всей оси Ох. Так как, то получаем ряд Если в разложении (1) заменить ж на -а*, то будем иметь Данная функция имеет производные любого порядка, причем. Тем самым, по теореме 8 функция sin ж разлагается в сходящийся к ней на интервале (-оо, +оо) ряд Тейлора. Так как то этот ряд имеет следующий вид Радиус сходимости ряда Аналогично получаем, что - любое действительное число Эта функция удовлетворяет соотношению и условию Будем искать степенной ряд, сумма которого 5(ж) удовлетворяет соотношению (4) и условию 5(0) = 1. Положим Отсюда находим Подставляя соотношения (5) и (6) в формулу (4), будем иметь Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства, получим откуда находим СТЕПЕННЫЕ РЯДЫ Теорема Абеля. Интервал и радиус сходимости степеннбго ряда Равномерная сходимость степенного ряда и непрерывность его суммы Интегрирование степенных рядов Дифференцирование степенных рядов Ряд Тейлора Условия разложимости функции в ряд Тейлора элементарных функций Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций. Подставляя эти значения коэффициентов в соотношение (5), получим ряд Найдем радиус сходимости ряда (7) в случае, когда а не является натуральным числом. Имеем Итак, ряд (7) сходится при. е. на интервале Докажем, что сумма 5(ж) ряда (7) на интервале (-1,1) равна (1 + ж)°. Для этого рассмотрим отношение Так как 5(х) удовлетворяет соотношению (то для производной функции ф(х) получаем: для. Отсюда следует, что. В частности, при х = 0 имеем и значит, или Полученный ряд называется биномиальным, а его коэффициенты - биномиальными коэффициентами. Замечание. В случае, если а - натуральное число (о = г»), функция (1 + z)a будет многочленом п-й степени, и Дп(х) = 0 для всех п > а. Отметим еще два разложения. При а = -1 будем иметь Заменив ж на -ж в последнем равенстве, получим получения разложения этой функции в ряд Тейлора по степеням ж проинтегрируем,енство (9) в пределах о Равенство (11) справедливо в интервале. Заменяя в нем ж на -ж, получим ряд Можно доказать, что равенство (11) справедливо и для ж = 1: Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций. Пользуясь этой таблицей, можно получать разложения в степенной ряд более сложных функций. Покажем на примерах, как это делается. Пример 1. Разложить функцию 4-х в степенной ряд в окрестности точки xq = 2, т. е. по степеням разности z -2. Преобразуем данную функцию так, чтобы можно было использовать ряд (10) для функции Имеем. Заменяя в формуле (10) х на ^. получим I I Это разложение справедливо, когда выполнено любое из эквивалентных неравенств Пример 2. Разложить по степеням х функцию используя формулу (10). 4 Разлагая знаменатель на множители, представим данную рациональную функцию в виде разности двух простейших дробей. После простых преобразований получим 1 К каждому слагаемому в правой части равенства (13) применяем формулу (10), в результате чего получим степенные ряды Ряд (14) сходится для \ а ряд (15) сходится для 2. Оба ряда (14) и (15) будут сходиться одновременно для \. Так как в интервале (-1,1) ряды (14) и (15) сходятся, то их можно почленно вычитать. В результате мы получим искомый степенной ряд радиус сходимости которого равен R = 1. Этот ряд сходится абсолютно для Пример 3. Разложить в ряд Тейлора в окрестности точки хо = 0 функцию arcsin х. 4 Известно, что Применим к функции (формулу (8). заменяя в ней х на -х2. В результате для получаем Интефируя обе части последнего равенства от нуля до х (почленное интегрирование законно, так как степенной ряд равномерно сходится на любом отрезке с концами в точках 0 и х, лежащем в интервале (-1,1)), найдем или Тем самым, окончательно получаем, что Замечание. Разложение в степенные ряды можно использовать для вычисления интегралов, не выражающихся в конечном виде через элементарные функции. Приведем несколько примеров. Пример 4. Вычислить интеграл (интегральный синус) , Известно, что первообразная для функции ^ не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, пользуясь тем, что Из равенства (16) находим Заметим, что деление ряда (16) на t при t ф О законно. Равенство (17) сохраняется и при если считать, что при t = О отношение - = 1. Тем самым, ряд (17) сходится при всех значениях. Интегрируя его почленно, получим Полученный ряд - знакочередующийся, так что погрешность при замене его суммы частичной суммой оценивается просто. Пример 5. Вычислить интеграл Здесь первообразная для подынтегральной функции е также не является элементарной функцией. Для вычисления интеграла заменим в формуле Получим Проинтегрируем обе части этого равенства в пределах от 0 до х: Этот ряд сходится при любых г (его радиус сходимости R = +оо) и является знакочередующимся при Упражнения Найдите область сходимости степенных рядов: Разложите следующие функции в ряд Маклореиа и укажите области сходимости полученных рядов: Указание. Воспользуйтесь таблицей. Пользуясь таблицей, разложите заданные функции в ряд Тейлора по степеням х - х0 и укажите интервалы сходимости полученных рядов.
Определение . Функциональный ряд вида
где ![]() … – действительные числа, называется степенным рядом.
… – действительные числа, называется степенным рядом.
Областью абсолютной сходимости ряда является интервал ![]() , где число R
– радиус сходимости.
, где число R
– радиус сходимости.
Пусть степенной ряд имеет радиус сходимости R > 0. Тогда справедливы следующие положения:
1. Сумма ряда является непрерывной функцией от x во всем интервале сходимости .
2. Ряд равномерно сходится на любом отрезке , где ![]() .
.
3. Ряд можно почленно интегрировать по любому отрезку , лежащему внутри интервала .
4. Ряд можно почленно дифференцировать в любой точке ![]() сколь угодно раз.
сколь угодно раз.
Примечания:
1. При почленном интегрировании или дифференцировании степенного ряда получаются новые степенные ряды, при этом их радиус сходимости остается тот же.
2. Радиус сходимости степенного ряда можно найти по одной из формул:
 , (10)
, (10)
 (11)
(11)
при условии, что указанные пределы существуют, – коэффициент ряда.
Задача 17.31
Найти сумму ряда  .
.
Решение:
I способ . Найдем интервал сходимости ряда:
, , ![]() .
.
Упростим рациональную дробь  ,
, ![]() .
.
Тогда ряд может быть представлен разностью двух рядов:
Сходимость каждого из них остается та же (убедитесь в этом самостоятельно). Поэтому равенство имеет место. Обозначим суммы рядов соответственно и , а искомую сумму – через , .
Найдем сумму первого ряда:
Дифференцируя почленно ряд внутри интервала сходимости , получим: ; представляет собой геометрическую прогрессию со знаменателем .
При прогрессия сходится, , , ![]() и сумма равна:
и сумма равна:  ;
;  . Теперь, интегрируя на отрезке , лежащем внутри интервала сходимости , получим:
. Теперь, интегрируя на отрезке , лежащем внутри интервала сходимости , получим:
 .
.
Найдем сумму второго ряда:
Выполним преобразование:
Обозначим сумму ряда, стоящего в скобках, через и продифференцируем в интервале :
– это тоже геометрическая прогрессия.
, ,  ;
;

 .
.
Итак, сумма исходного ряда равна:
 или
или
для ![]() .
.
II способ
. Не повторяя подробностей I способа, связанных с интервалом сходимости данного ряда, предлагаем II вариант решения задачи. Обозначим сумму ряда через :  .
.
Умножим на данный ряд:  . Продифференцируем дважды полученный ряд:
. Продифференцируем дважды полученный ряд:
 ,
,
Представляет собой геометрическую прогрессию со знаменателем ![]() , тогда
, тогда  . Проинтегрируем на отрезке :
. Проинтегрируем на отрезке :
Интегрируя по частям, получим:
для ![]() .
.
Задача 18.31
Найти сумму ряда  .
.
Решение:
Данный ряд сходится в интервале (убедитесь в этом самостоятельно). Перепишем его, представив в виде суммы трех рядов:
Это возможно, так как каждый из рядов имеет одну и ту же область сходимости – интервал . Обозначим суммы трех рядов соответственно через , , , а искомую сумму – через .
как сумма членов геометрической прогрессии со знаменателем ![]()
Выполним преобразование:
Обозначим через сумму ряда .
Интегрируя почленно этот ряд на отрезке внутри интервала сходимости , получим:
Чтобы найти , надо продифференцировать дробь :
 .
.
Следовательно,  .
.
Теперь найдем :
Вынесем за скобки:
Обозначим через сумму ряда, стоящего в скобках. Тогда
В этих скобках стоит ряд, сумма которого найдена:  . Получаем:
. Получаем:  .
.
Но ![]() ,
,  . Тогда сумма исходного ряда
. Тогда сумма исходного ряда
Итак,  для
для ![]() .
.
Ряд Тейлора
Определение
. Ряд 
называется рядом Тейлора по степеням для функции .
Функция может быть разложена в ряд Тейлора, если в рассматриваемой точке она имеет производные всех порядков и если остаточный член в точке при стремится к нулю. При ряд Тейлора называют иногда рядом Маклорена.
Теорема
Если функция разлагается в степенной ряд, то для неё этот ряд единственный и является рядом Тейлора.
Примечание . Находя последовательно производные функции и их значения в точке , можно записать ряд Тейлора. Но при этом исследование остаточного члена представляет большие трудности. Поэтому часто идут другим путем: пользуются готовыми разложениями основных элементарных функций в степенные ряды в комбинациях с правилами сложения, вычитания, умножения рядов и теоремами об их интегрировании и дифференцировании, как это, например, было показано в задачах 17.31 и 18.31.
Задача 19.31
Разложить функцию  в ряд Тейлора по степеням .
в ряд Тейлора по степеням .
Решение:
х 0 = 0. Воспользуемся примечанием. Так как
то функция упрощается, если применить метод неопределенных коэффициентов:
 .
.
Сумма членов геометрической прогрессии со знаменателем равна:  . В нашем случае
. В нашем случае  . – радиус сходимости этого ряда. Слагаемое ,
. – радиус сходимости этого ряда. Слагаемое ,
Складывая ряды, получим: или  , где – общая область сходимости. целиком лежит в области сходимости ряда .
, где – общая область сходимости. целиком лежит в области сходимости ряда .
Чтобы вычислить данный интеграл с точностью до 0,001, надо взять в полученном ряде два его члена (0,0005<0,001) (см. задачу 9.31).
Таким образом,
Вопросы для самопроверки
Числовые ряды
1. Дайте определения сходящихся и расходящихся рядов.
2. Сформулируйте необходимый признак сходимости ряда.
3. Сформулируйте достаточные признаки сходимости рядов с положительными членами: сравнение рядов с положительными членами; признак Даламбера; радикальный признак Коши, интегральный признак Коши.
4. Дайте определение абсолютно сходящегося ряда. Сформулируйте свойства абсолютно сходящихся рядов.
5. Сформулируйте признак Лейбница.
Функциональные ряды
6. Дайте определение области сходимости функционального ряда.
7. Какой ряд называется равномерно сходящимся?
8. Сформулируйте признак Вейерштрасса.
9. Условия разложимости функции в ряд Тейлора.
10. Сформулируйте теоремы об интегрировании и дифференцировании степенных рядов.
11. Изложите метод приближенного вычисления определенных интегралов с помощью рядов.
1. Кудрявцев Л.Д. Краткий курс математического анализа. – М.: Наука, 1989. – 736 с.
2. Бугров Я.С. Дифференциальное и интегральное исчисления /Я.С. Бугров, С.М. Никольский. – М.: Наука, 1984. – 432 с.
3. Шмелев П.А. Теория рядов в задачах и упражнениях. – М.: Высшая школа, 1983. – 176 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Наука, 1985. – 576 с.
5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. – М.: Физматгиз, 1962. – 808 с.
6. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966. – 460 с.
7. Кузнецов Л.А. Сборник заданий по высшей математике (ТР). – М.: Высшая школа, 1983. – 174 с.
8. Данко П.Е. Высшая математика в упражнениях и задачах. Ч. 2 /П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 1986. – 415 с.
9. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 1986. – 544 с.
Учебное издание
Бородин Николай Павлович
Жернова Варвара Викторовна
Шуметова Людмила Викторовна
Шоркин Владимир Сергеевич
РЯДЫ
Учебно-методическое пособие
Редактор Т.Д. Васильева
Технический редактор Т.П. Прокудина
Орловский государственный технический университет
Лицензия ИД № 00670 от 05.01.2000
Подписано к печати 26.08.2004 г. Формат 60 x 84 1/16.
Печать офсетная. Уч.-изд. л. 1,9. Усл. печ. л. 2,4. Тираж 500 экз.
Заказ №____
Отпечатано с готового оригинал-макета
на полиграфической базе ОрелГТУ,
302030, г. Орел, ул. Московская, 65.
Ряды.
Основные определения.
Определение. Сумма членов бесконечной числовой последовательности называется числовым рядом .
При этом числа будем называть членами ряда, а u n – общим членом ряда.
Определение. Суммы , n = 1, 2, … называются частными (частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S 1 , S 2 , …,S n , …
Определение. Ряд называется сходящимся , если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда и , где С – постоянное число.
Теорема. Если ряд сходится и его сумма равна S, то ряд тоже сходится, и его сумма равна СS. (C ¹ 0)
3) Рассмотрим два ряда и . Суммой или разностью этих рядов будет называться ряд , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды и сходятся и их суммы равны соответственно S и s, то ряд тоже сходится и его сумма равна S + s.
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.
(необходимые и достаточные условия сходимости ряда)
Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы для любого существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
Доказательство. (необходимость)
Пусть , тогда для любого числа найдется номер N такой, что неравенство
Выполняется при n>N. При n>N и любом целом p>0 выполняется также неравенство . Учитывая оба неравенства, получаем:
Необходимость доказана. Доказательство достаточности рассматривать не будем.
Сформулируем критерий Коши для ряда.
Для того, чтобы ряд был сходящимся необходимо и достаточно, чтобы для любого существовал номер N такой, что при n>N и любом p>0 выполнялось бы неравенство
Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому как правило используются более простые признаки сходимости:
1) Если ряд сходится, то необходимо, чтобы общий член u n стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд является расходящимся, хотя его общий член и стремится к нулю.
Пример. Исследовать сходимость ряда
Найдем - необходимый признак сходимости не выполняется, значит ряд расходится.
2) Если ряд сходится, то последовательность его частных сумм ограничена.
Однако, этот признак также не является достаточным.
Например, ряд 1-1+1-1+1-1+ … +(-1) n+1 +… расходится, т.к. расходится последовательность его частных сумм в силу того, что
Однако, при этом последовательность частных сумм ограничена, т.к. при любом n .
Ряды с неотрицательными членами.
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.
Теорема. Для сходимости ряда с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены .
Признак сравнения рядов с неотрицательными членами.
Пусть даны два ряда и при u n , v n ³ 0 .
Теорема. Если u n £ v n при любом n , то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .
Доказательство. Обозначим через S n и s n частные суммы рядов и . Т.к. по условию теоремы ряд сходится, то его частные суммы ограничены, т.е. при всех n s n < M, где М – некоторое число. Но т.к. u n £ v n , то S n £ s n то частные суммы ряда тоже ограничены, а этого достаточно для сходимости.
Пример.
Т.к. , а гармонический ряд расходится, то расходится и ряд .
Пример. Исследовать на сходимость ряд
Т.к. , а ряд сходится (как убывающая геометрическая прогрессия), то ряд тоже сходится.
Также используется следующий признак сходимости:
Теорема. Если и существует предел , где h – число, отличное от нуля, то ряды и ведут одинаково в смысле сходимости.
Признак Даламбера.
(Жан Лерон Даламбер (1717 – 1783) – французский математик)
Если для ряда с положительными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство
то ряд сходится, если же для всех достаточно больших n выполняется условие
то ряд расходится.
Предельный признак Даламбера.
Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.
< 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
Пример. Определить сходимость ряда .
Вывод: ряд сходится.
Пример. Определить сходимость ряда
Вывод: ряд сходится.
Признак Коши. (радикальный признак)
Если для ряда с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство
то ряд сходится, если же для всех достаточно больших n выполняется неравенство
то ряд расходится.
Следствие. Если существует предел , то при r<1 ряд сходится, а при r>1 ряд расходится.
Пример. Определить сходимость ряда .
Вывод: ряд сходится.
Пример. Определить сходимость ряда .
Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Интегральный признак Коши.
Если j(х) – непрерывная положительная функция, убывающая на промежутке и то интегралы и ведут себя одинаково в смысле сходимости.
Знакопеременные ряды.
Знакочередующиеся ряды.
Знакочередующийся ряд можно записать в виде:
Признак Лейбница.
Если у знакочередующегося ряда абсолютные величины u i убывают и общий член стремится к нулю , то ряд сходится.
Абсолютная и условная сходимость рядов.
Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).
и ряд, составленный из абсолютных величин членов ряда (1):
Теорема. Из сходимости ряда (2) следует сходимость ряда (1).
Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого e>0 существует число N, такое, что при n>N и любом целом p>0 верно неравенство:
По свойству абсолютных величин:
То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).
Определение. Ряд называется абсолютно сходящимся , если сходится ряд .
Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд называется условно сходящимся , если он сходится, а ряд расходится.
Признаки Даламбера и Коши для знакопеременных рядов.
Пусть - знакопеременный ряд.
Признак Даламбера. Если существует предел , то при r<1 ряд будет абсолютно сходящимся, а при r>
Признак Коши. Если существует предел , то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Свойства абсолютно сходящихся рядов.
1) Теорема. Для абсолютной сходимости ряда необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами .
Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.
2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.
3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.
Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда .
5) Если ряды и сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.
Функциональные последовательности.
Определение. Если членами ряда будут не числа, а функции от х , то ряд называется функциональным .
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х , при которых ряд сходится.
Совокупность таких значений называется областью сходимости .
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
Определение. Последовательность {f n (x) } сходится к функции f(x) на отрезке , если для любого числа e>0 и любой точки х из рассматриваемого отрезка существует номер N = N(e, x), такой, что неравенство
выполняется при n>N.
При выбранном значении e>0 каждой точке отрезка соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка , будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка , т.е. будет общим для всех точек.
Определение. Последовательность {f n (x) } равномерно сходится к функции f(x) на отрезке , если для любого числа e>0 существует номер N = N(e), такой, что неравенство
выполняется при n>N для всех точек отрезка .
Пример. Рассмотрим последовательность
Данная последовательность сходится на всей числовой оси к функции f(x)=0 , т.к.
Построим графики этой последовательности:
Как видно, при увеличении числа n график последовательности приближается к оси х .
Функциональные ряды.
Определение. Частными (частичными) суммами функционального ряда называются функции
Определение. Функциональный ряд называется сходящимся в точке (х=х 0 ), если в этой точке сходится последовательность его частных сумм. Предел последовательности называется суммой ряда в точке х 0 .
Определение. Совокупность всех значений х , для которых сходится ряд называется областью сходимости ряда.
Определение. Ряд называется равномерно сходящимся на отрезке , если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
выполнялось бы для всех х на отрезке .
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд сходится равномерно и притом абсолютно на отрезке , если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами:
т.е. имеет место неравенство:
Еще говорят, что в этом случае функциональный ряд мажорируется числовым рядом .
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку , сходится к интегралу от суммы ряда по этому отрезку .
3) Теорема о почленном дифференцировании ряда.
Если члены ряда сходящегося на отрезке представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
На основе того, что сумма ряда является некоторой функцией от переменной х , можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)
Теорема. Если степенной ряд сходится при x = x 1 , то он сходится и притом абсолютно для всех .
Доказательство. По условию теоремы, так как члены ряда ограничены, то
где k - некоторое постоянное число. Справедливо следующее неравенство:
Из этого неравенства видно, что при x
Поэтому на основании признака сравнения делаем вывод, что ряд сходится, а значит ряд
Рассмотрим функциональный ряд$\sum \limits _{n=1}^{\infty }u_{n} (x)=u_{1} (x)+u_{2} (x)+u_{3} (x)+...$, члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда $S_{n} (x)=u_{1} (x)+u_{2} (x)+...+u_{n} (x)$ является частичной суммой данного функционального ряда. Общий член $u_{n} (x)$ есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке $x=x_{0} $. Если соответствующий числовой ряд $\sum \limits _{n=1}^{\infty }u_{n} (x_{0})$сходится, т.е. существует предел частичных сумм этого ряда$\mathop{\lim }\limits_{n\to \infty } S_{n} (x_{0})=S(x_{0})$(где $S(x_{0})
Определение 2
Областью сходимости функционального ряда $\sum \limits _{n=1}^{\infty }u_{n} (x)$ называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается $D(x)$. Отметим, что $D(x)\subset $R.
Функциональный ряд сходится в области $D(x)$, если для любого $x\in D(x)$ он сходится как числовой ряд, при этом его сумма будет некоторой функцией $S(x)$. Это так называемая предельная функция последовательности $\left\{S{}_{n} (x)\right\}$: $\mathop{\lim }\limits_{n\to \infty } S_{n} (x)=S(x)$.
Как находить область сходимости функционального ряда $D(x)$? Можно использовать признак, аналогичный признаку Даламбера. Для ряда $\sum \limits _{n=1}^{\infty }u_{n} (x)$ составляем $u_{n+1} (x)$ и рассматриваем предел при фиксированном х: $\mathop{\lim }\limits_{n\to \infty } \left|\frac{u_{n+1} (x)}{u_{n} (x)} \right|=\left|l(x)\right|$. Тогда $D(x)$ является решением неравенства $\left|l(x)\right|
Пример 1
Найти область сходимости ряда $\sum \limits _{n=1}^{\infty }\, \frac{x^{n} }{n} \, $.
Решение. Обозначим $u_{n} (x)=\frac{x^{n} }{n} $, $u_{n+1} (x)=\frac{x^{n+1} }{n+1} $. Составим и вычислим предел $\mathop{\lim }\limits_{n\to \infty } \left|\frac{u_{n+1} (x)}{u_{n} (x)} \right|=\mathop{\lim }\limits_{n\to \infty } \left|\frac{x^{n+1} \cdot n}{x^{n} \cdot (n+1)} \right|=\left|x\right|$, тогда область сходимости ряда определяется неравенством $\left|x\right|
если $x=1$, $u_{n} (1)=\frac{1}{n} $, то получается расходящийся ряд $\sum \limits _{n=1}^{\infty }\, \frac{1}{n} \, $;
если $x=-1$, $u_{n} (-1)=\frac{(-1)^{n} }{n} $, то ряд $\sum \limits _{n=1}^{\infty }\frac{(-1)^{n} }{n} \, \, $ сходится условно (по признаку Лейбница).
Таким образом, область сходимости $D(x)$ ряда $\sum \limits _{n=1}^{\infty }\, \frac{x^{n} }{n} \, $имеет вид:$-1\le x
Свойства степенных рядов
Рассмотрим степенной ряд $\sum \limits _{n=0}^{\infty }a_{n} x^{n} $, у которого интервал сходимости $(-R;\, R)$, тогда сумма степенного ряда $S(x)$ определена для всех $x\in (-R;R)$ и можно записать равенство $S(x)=\sum \limits _{n=0}^{\infty }a_{n} x^{n} $.
Свойство 1. Степенной ряд $\sum \limits _{n=0}^{\infty }a_{n} x^{n} $ сходится абсолютно в любом промежутке $\, \, \subset \, (-R;R)$, лежащем в интервале сходимости, причём сумма степенного ряда $S(x)$ является непрерывной функцией при всех $x\in $.
Свойство 2. Если отрезок $\, \, \subset \, (-R;R)$, то степенной ряд можнопочленно интегрировать от a до b, т.е. если
$S(x)=\sum \limits _{n=0}^{\infty }a_{n} x^{n} =a_{0} +a_{1} x+a_{2} x^{2} +...$, то
$\int \limits _{a}^{b}S(x)\, {\rm d}x =\sum \limits _{n=0}^{\infty }\int \limits _{a}^{b}a_{n} x^{n} \, {\rm d}x=\int \limits _{a}^{b}a_{0} {\rm d}x +\int \limits _{a}^{b}a_{1} x\, {\rm d}x +...+\int \limits _{a}^{b}a_{n} x^{n} \, {\rm d}x +...$.
При этом радиус сходимости не меняется:
где $a"_{n} =\frac{a_{n} }{n+1} $ - коэффициенты проинтегрированного ряда.
Свойство 3. Сумма степенного ряда есть функция, имеющая внутри интервала сходимости производные любого порядка. Производные от суммы степенного ряда будут суммами рядов, полученных из данного степенного ряда почленным дифференцированием соответствующее число раз, причём радиусы сходимости таких рядов будут те же, что и у исходного ряда.
Если $S(x)=a_{0} +a_{1} x+a_{2} x^{2} +...+a_{n} x^{n} +...=\sum \limits _{n=0}^{\infty }\, a_{n} \cdot x^{n} $,то $S"(x)=a_{1} +2a_{2} x+...+na_{n} x^{n-1} +...=\sum \limits _{n=1}^{\infty }\, n\cdot a_{n} \cdot x^{n-1} $,$S""(x)=2a_{2} +6a_{3} x+...+n(n-1)a_{n} x^{n-2} +...=\sum \limits _{n=2}^{\infty }\, n\cdot (n-1)\cdot a_{n} \cdot x^{n-2} $, ... , и т.д.
Примеры
Ряд $\sum \limits _{n=1}^{\infty }n!\; x^{n} $ сходится только в точке $x=0$, во всех остальных точках ряд расходится. $V:\left\{0\right\}.$
Ряд $\sum \limits _{n=1}^{\infty }\frac{x^{n} }{n!} $ сходится во всех точках оси, $V=R$.
Ряд $\sum \limits _{n=1}^{\infty }\frac{(-1)^{n} x^{n} }{n} $ сходится в области $V=(-1,\, 1]$.
Ряд $\sum \limits _{n=1}^{\infty }\frac{1}{n+\cos x} $ расходится во всех точках оси $V=$$\emptyset$.
Элементы семантической структуры
Семантическая структура предложения.
(этот вопрос – на самостоятельное изучение!)
Этот тип анализа связывает смысловую организацию предложения с его формальной организацией. Это направление выдвинуло понятие семантической структуры предложения (прежде всего – Н.Ю. Шведова).
Структурная схема имеет свою семантику, которая создается формальными значениями компонентов, правилами их лексического наполнения и отношением компонентов друг к другу (в неоднокомпонентных схемах).
Языковое значение построенного по тому или другому образцу конкретного предложения формируется взаимным действием семантики этого образца и лексической семантики тех слов, которые заняли позиции его компонентов: Ученик пишет; ребенок радуется при общей семантике МСС («отношение между субъектом и его предикативным признаком – действием или процессуальным состоянием») в первом случает представлено значение «отношение между субъектом и его конкретным действием», во втором случае – «отношение между субъектом и его эмоциональным состоянием».
Функциональные ряды вида где (коэффициенты ряда) и (центр ряда) – постоянные, переменная, называются степенными рядами. Ясно, что если мы научимся вычислять область сходимости степенного ряда (с центром), то легко найдем и область сходимости исходного ряда Поэтому впредь, если не оговорено противное, будем рассматривать степенные ряды вида.
Теорема Абеля. Если степенной ряд сходится в точке то он сходится абсолютно и в интервале На любом отрезке указанный ряд сходится равномерно.
Доказательство. Поскольку ряд сходится, то его общий член поэтому последовательность ограничена, т.е. существует постоянная такая, что
Пусть теперь. Тогда будем иметь
Поскольку геометрическая прогрессия сходится (), то по первой теореме сравнения сходится и ряд Первая часть теоремы доказана.
Так как по доказанному ряд сходится и он мажорирует при (см.) ряд, то по теореме Вейерштрасса последний ряд сходится равномерно при Теорема полностью доказана.
Из теоремы Абеля вытекает, что мы можем расширять интервал до тех пор пока не настанет момент, когда в точке ряд будет расходиться (или такой момент вообще не настанет, т.е.). Тогда указанный интервал будет областью сходимости ряда Таким образом, любой степенной ряд имеет в качестве области сходимости не произвольное множество, а именно интервал. Дадим более точное определение интервала сходимости.
Определение 2. Число называется радиусом сходимости ряда, если внутри интервала этот ряд сходится абсолютно , а вне отрезка он расходится. При этом интервал называется интервалом сходимости ряда.
Заметим, что при указанный степенной ряд сходится только в точке а при он сходится при всех действительных Следующие примеры показывают, что эти случаи не исключаются: Примером ряда с ненулевым конечным радиусом сходимости может служить геометрическая прогрессия Заметим также, что на границе интервала сходимости степенной ряд может как сходиться, так и расходиться. Например, ряд сходится условно в точке и расходится в точке
Из свойств равномерно сходящихся функциональных рядов (теоремы 1-3) легко выводятся следующие свойства степенных рядов.
Теорема 4. Пусть – радиус сходимости степенного ряда. Тогда имеют место следующие высказывания:
1. Сумма данного степенного ряда непрерывна в интервале сходимости;
2. Если – радиус сходимости степенного ряда, то ряд из производных будет иметь тот же радиус сходимости Отсюда вытекает, что степенной ряд можно дифференцировать сколько угодно раз (т.е. его сумма бесконечно дифференцируема в интервале сходимости), причем имеет место равенство
3. Степенной ряд можно интегрировать на любом отрезке лежащем внутри его интервала сходимости, т.е.
Доказательство , например, первого свойства будет таким. Пусть произвольная точка интервала сходимости . Окружим эту точку симметричным отрезком По теореме Абеля ряд сходится равномерно на отрезке, поэтому его сумма непрерывна на указанном отрезке, а значит, непрерывна, в частности, и в точке Свойство 1 доказано. Аналогично доказываются и остальные свойства нашей теоремы.
Теперь займемся вычислением радиуса сходимости степенного ряда по его коэффициентам.
Теорема 4. Пусть выполнено хотя бы одно из следующих условий:
а) существует (конечный или бесконечный) предел
б) существует (конечный или бесконечный) предел (при этом предполагается, существует номер такой, что).
Тогда число радиус сходимости ряда.
Доказательство проведем для случая а). Применим к модульному ряду признак Коши: По указанному признаку ряд сходится абсолютно, если число т.е. если Если же т.е. если то указанный ряд расходится. Следовательно, радиус сходимости ряда. Теорема доказана.
Замечание 1. Теорема 1-4 практически без изменения формулировок переносятся и на степенные ряды вида (с небольшой поправкой, что в этом случае областью сходимости является интервал).
Пример 1. Найти область сходимости ряда (задача 10, Т.Р., Кузнецов Л.А.)
Решение. Применим аналог а) теоремы Коши: радиус сходимости данного ряда. Значит, ряд сходится абсолютно в области
Исследуем сходимость ряда на концах интервала. Имеем
расходится, т.к.
расходится, т.к.
Следовательно, областью сходимости исходного ряда является интервал.