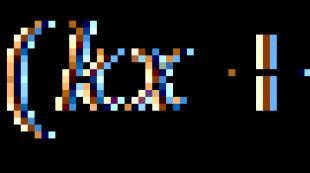Глаголы

Как объяснить давление газа на стенки сосуда. Давление газа на стенки сосуда. Закон Дальтона. Повторение пройденного материала

Мы уже говорили (§ 220), что газы всегда нацело заполняют объем, ограниченный непроницаемыми для газа стенками. Так, например, стальной баллон, употребляемый в технике для хранения сжатых газов (рис. 375), или камера автомобильной шины полностью и практически равномерно заполнены газом.

Рис. 375. Стальной баллон для хранения сильно сжатых газов

Стремясь расшириться, газ оказывает давление на стенки баллона, камеры шины или любого другого тела, твердого или жидкого, с которым он соприкасается. Если не принимать во внимание действия поля тяжести Земли, которое при обычных размерах сосудов лишь ничтожно меняет давление, то при равновесии давление газа в сосуде представляется нам совершенно равномерным. Это замечание относится к макромиру. Если же представить себе, что происходит в микромире молекул, составляющих газ в сосуде, то ни о каком равномерном распределении давления не может быть и речи. В одних местах поверхности стенок молекулы газа ударяют о них, в то время как в других местах удары отсутствуют; эта картина все время беспорядочным образом меняется.

Допустим для простоты, что все молекулы до удара о стенку летят с одинаковой скоростью , направленной по нормали к стенке. Будем также считать удар абсолютно упругим. При этих условиях скорость молекулы при ударе будет изменять направление на обратное, оставаясь неизменной по модулю. Следовательно, скорость молекулы после удара будет равна . Соответственно импульс молекулы до удара равен , а после удара он равен ( - масса молекулы). Вычтя из конечного значения импульса его начальное значение, найдем сообщаемое стенкой приращение импульса молекулы. Оно равно . Согласно третьему закону Ньютона стенке сообщается при ударе импульс, равный .

Если за единицу времени на единицу площади стенки приходится ударов, то за время об участок поверхности стенки ударяют молекул. Молекулы сообщают участку за время суммарный импульс, равный по модулю . В силу второго закона Ньютона этот импульс равен произведению силы , действующей на участок , на время . Таким образом,

Откуда .

Разделив силу на площадь участка стенки , получим давление газа на стенку:

Нетрудно сообразить, что число ударов в единицу времени зависит от скорости молекул, ибо чем быстрее они летят, тем чаще ударяются о стенку, и от числа молекул в единице объема, ибо чем больше молекул, тем больше и число наносимых ими ударов. Следовательно, можно считать, что пропорционально и , т. е. пропорционально

Для того чтобы рассчитать с помощью молекулярной теории давление газа, мы должны знать следующие характеристики микромира молекул: массу , скорость и число молекул в единице объема. Для того чтобы найти эти микрохарактеристики молекул, мы должны установить, от каких характеристик макромира зависит давление газа, т. е. установить на опыте законы газового давления. Сравнив эти опытные законы с законами, рассчитанными при помощи молекулярной теории, мы получим возможность определить характеристики микромира, например скорости газовых молекул.

Итак, установим, от чего зависит давление газа?

Во-первых, давление зависит от степени сжатия газа, т. е. оттого, сколько молекул газа находится в данном объеме. Например, нагнетая в автомобильную шину все больше воздуха или сжимая (уменьшая объем) закрытую камеру, мы заставляем газ все сильнее давить на стенки камеры.

Во-вторых, давление зависит от температуры газа. Известно, например, что мяч становится более упругим, если его подержать вблизи нагретой печи.

Обычно изменение давления вызывается обеими причинами сразу: и изменением объема, и изменением температуры. Но можно осуществить процесс так, что при изменении объема температура будет меняться ничтожно мало или при изменении температуры объем практически останется неизменным. Этими случаями мы сперва и займемся, сделав предварительно еще следующее замечание. Мы будем рассматривать газ в состоянии равновесия. Это значит, что в газе установилось как механическое, так и тепловое равновесие.

Механическое равновесие означает, что не происходит движения отдельных частей газа. Для этого необходимо, чтобы давление газа было во всех его частях одинаково, если пренебречь незначительной разницей давления в верхних и нижних слоях газа, возникающей под действием силы тяжести.

Тепловое равновесие означает, что не происходит передачи теплоты от одного участка газа к другому. Для этого необходимо, чтобы температура во всем объеме газа была одинакова.

Класс: 7

Презентация к уроку

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Учебник «Физика. 7 кл.» А.В. Перышкин – М. : Дрофа, 2011 г.

Тип урока: комбинированный на основе исследовательской деятельности.

Цели:

установить причину существования давления в газах с точки зрения молекулярного строения вещества;
выяснить:
от чего зависит давление газа
как можно его изменить.

Задачи:

сформировать знания о давлении газа и природе возникновения давления на стенки сосуда, в котором находится газ;
сформировать умение объяснять давление газа на основе учения о движении молекул, зависимости давления от объема при постоянной массе и температуре, а также и при изменении температуры;
развить общеучебные знания и умения: наблюдать, делать выводы;
способствовать привитию интереса к предмету, развития внимания, научного и логического мышления учащихся.

Оборудование и материалы к уроку: компьютер, экран, мультимедиапроектор, презентация к уроку, колба с пробкой, штатив, спиртовка, шприц, воздушный шар, пластиковая бутылка с пробкой.

План урока:

Проверка домашнего задания.
Актуализация знаний.
Объяснение нового материала.
Закрепление пройденного материала на уроке.
Итог урока. Домашнее задание.

ХОД УРОКА

Я предпочитаю то, что можно увидеть, услышать и изучить. (Гераклит) (Слайд 2)

– Это девиз нашего урока

– На прошлых уроках мы с вами узнали о давлении твердых тел, от каких физических величин зависит давление.

1. Повторение пройденного материала

1. Что такое давление?
2. От чего зависит давление твердого тела?
3. Как давление зависит от силы, приложенной перпендикулярно опоре? Каков характер этой зависимости?
4. Как давление зависит от площади опоры? Каков характер этой зависимости?
5. В чем причина давления твердого тела на опору?

Качественная задача.

Одинаковы ли силы, действующие на опору, и давление в обоих случаях? Почему?

Проверка знаний. Тестирование (проверка и взаимопроверка)

Тест

1. Физическая величина, имеющая размерность паскаль (Па), называется:

а) сила; б) масса; в) давление; г) плотность.

2. Силу давления увеличили в 2 раза. Как изменится давление?

а) уменьшится в 2 раза; б) останется прежним; в) увеличится в 4 раза; г) увеличится в 2 раза.

4. Какое давление на пол оказывает ковёр весом 200 Н, площадью 4 м 2 ?

а) 50 Па; б) 5 Па; в) 800Па; г) 80 Па.

5. Два тела равного веса поставлены на стол. Одинаковое ли давление они производят на стол?

2. Актуализация знаний (в форме беседы)

– Почему воздушные шары и мыльные пузыри круглые?
Учащиеся надувают воздушные шары.
– Чем мы заполнили шары? (Воздухом) Чем еще можно заполнить шары? (Газами)
– Предлагаю сжать шары. Что вам мешает сжать шары? Что действует на оболочку шара?
– Возьмите пластиковые бутылки, закройте пробкой и попробуйте сжать.
– О чем пойдет речь на уроке?

– Тема урока: Давление газа

3. Объяснение нового материала

Газы, в отличии от твёрдых тел и жидкостей, заполняют весь сосуд, в котором находятся.
Стремясь расшириться, газ оказывает давление на стенки, дно и крышку любого тела, с которым он соприкасается.
(Слайд 9) Картинки стальных баллонов, в которых находится газ; камеры автомобильной шины; мяча
Давление газа обусловлено иными причинами, чем давление твердого тела на опору.

Вывод: давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см 2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, оно и создает давление газа.
Учащиеся самостоятельно работают с учебником. Читают опыт с резиновым шаром под колоколом. Как объяснить этот опыт? (стр.83 рис. 91)

Учащиеся объясняют опыт.

(Слайд 11) Просмотр видеофрагмента с объяснением опыта для закрепления материала.

(Слайд 12) Минутка отдыха. Зарядка для глаз.

«Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели настоящей науки».

Альберт Эйнштейн

(Слайд 14) ИМЕЮТ ЛИ ГАЗЫ ОБЪЁМ? ЛЕГКО ЛИ ИЗМЕНИТЬ ОБЪЁМ ГАЗОВ? ЗАНИМАЮТ ЛИ ГАЗЫ ВЕСЬ ПРЕДОСТАВЛЯЕМЫЙ ИМ ОБЪЁМ? ПОЧЕМУ?ПОЧЕМУ? ИМЕЮТ ЛИ ГАЗЫ ПОСТОЯННЫЙ ОБЪЁМ И СОБСТВЕННУЮ ФОРМУ? ПОЧЕМУ?

рис. 92 стр. 84

(Слайд 15) У учащихся сделаны модели из шприцов. Выполнение опыта.
Учащиеся делают вывод: при уменьшении объёма газа его давление увеличивается, а при увеличении объёма давление уменьшается при условии, что масса и температура газа остаются неизменными.

(Слайд 16) Опыт с колбой

– Как изменится давление газа, если нагреть его при постоянном объеме?
При нагревании давление газа в колбе будет постепенно возрастать до тех пор, пока пробка не вылетит из склянки.
Учащиеся делают вывод: давление газа в закрытом сосуде тем больше, чем выше температура газа,при условии, что масса газа и объём не изменяются. (Слайд 17)

Газы, заключенные в сосуде, можно сжимать или сдавливать, уменьшая при этом их объем. Сжатый газ равномерно распределяется во всех направлениях. Чем сильнее вы сжимаете газ, тем выше будет его давление.
Учащиеся делают вывод: давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда

4. Закрепление пройденного материала на уроке.

(Слайд 18) Подумай-ка

– Что происходит с молекулами газа при уменьшении объёма сосуда, в котором находится газ?

молекулы начинают быстрее двигаться,
молекулы начинают медленнее двигаться,
среднее расстояние между молекулами газа уменьшается,
среднее расстояние между молекулами газа увеличивается.

(Слайд 19) Сравни-ка свои ответы

Чем вызвано давление газа?
Почему давление газа увеличивается при его сжатии и уменьшается при расширении?
Когда давление газа больше: в холодном или горячем состоянии? Почему?

Ответ 1. Давление газа вызвано ударами молекул газа о стенки сосуда или о помещенное в газ тело
Ответ 2. При сжатии плотность газа увеличивается, из-за чего возрастает число ударов молекул о стенки сосуда. Следовательно, увеличивается и давление. При расширении плотность газа уменьшается, что влечет за собой уменьшение числа ударов молекул о стенки сосуда. Поэтому давление газа уменьшается
Ответ 3. Давление газа больше в горячем состоянии. Это связано с тем, что молекулы газа при повышении температуры начинают двигаться быстрее, из-за чего удары их становятся чаще и сильнее.

(Слайд 20) Качественные задачи. (Сборник задач по физике В.И. Лукашик, Е.В.Иванова, Москва «Просвещение» 2007 г. стр. 64)

1. Почему при накачивании воздуха в шину автомобиля с каждым разом становится все труднее двигать ручку насоса?

2. Массы одного и того же газа, находящегося в разных закрытых сосудах при одинаковой температуре, одинаковы. В каком из сосудов давление газа наибольшее? Наименьшее? Ответ объясните

3. Объясните появление вмятины на мяче

Мяч при комнатной температуре

Мяч на снегу в морозный день

Решать загадки можно вечно.
Вселенная ведь бесконечна.
Спасибо всем нам за урок,
А главное, чтоб был он впрок!

Рефлексия.

5. Итог урока

Домашнее задание: §35

Мякишев Г.Я. Давление газа в сосуде //Квант. - 1987. - № 9. - С. 41-42.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Зависит ли давление газа на стенку сосуда от материала стенки и ее температуры? Попробуем ответить на этот вопрос.

При выводе основного уравнения молекулярно-кинетической теории идеального газа в учебнике «Физика 9» (§7) предполагается, что стенка абсолютно гладкая и столкновения молекул со стенкой происходят по закону абсолютно упругого удара. Другими словами, кинетическая энергия молекулы при ударе не меняется, и угол падения молекулы равен углу отражения. Является ли это предположение оправданным и необходимым?

Коротко можно сказать так: предположение оправдано, но не необходимо.

На первый взгляд кажется, что считать стенку абсолютно гладкой ни в коем случае нельзя - стенка сама состоит из молекул и, значит, гладкой быть не может. Из-за этого угол падения.не может при любом соударении равняться углу отражения. Кроме того, молекулы стенки совершают хаотические колебания около положений равновесия (участвуют в беспорядочном тепловом движении). Поэтому при столкновении с какой-либо молекулой стенки молекула газа может передать часть энергии стенке или, наоборот, увеличить свою кинетическую энергию за счет стенки.

Тем не менее предположение об абсолютно упругом характере соударения молекулы газа со стенкой оправдано. Дело в том, что при вычислении давления в конечном счете важны средние значения соответствующих величин. При условии теплового равновесия между газом и стенкой сосуда кинетическая энергия молекул газа в среднем остается неизменной, т. е. соударения со стенкой не меняют среднюю энергию молекул газа. Если бы это было не так, то тепловое равновесие самопроизвольно нарушалось бы. А это невозможно согласно второму закону термодинамики. Также не может быть преимущественного отражения молекул в каком-либо определенном направлении - иначе сосуд с газом начал бы двигаться, что противоречит закону сохранения импульса. Значит, среднее число молекул, падающих на стенку под некоторым углом, равно среднему числу молекул, отлетающих от стенки под таким же углом. Предположение о зеркальном отражении от стенки каждой отдельной молекулы соответствует этому условию.

Таким образом, считая соударения молекул газа со стенкой упругими, мы получаем для среднего давления такой же результат, как и без этого предположения. Значит, давление газа не зависит от качества обработки стенки (ее гладкости). Однако предположение об абсолютно упругом характере удара сильно упрощает вычисление давления газа, и поэтому оно оправдано.

А зависит ли давление газа на стенку от ее температуры? На первый взгляд - должно зависеть. Если, например, нет теплового равновесия, то молекулы от холодной стенки должны отскакивать с меньшей энергией, чем от горячей.

Однако, даже если одну стенку поддерживать холодной с помощью холодильной установки, то давление на нее все равно не может быть меньше, чем давление на противоположную горячую стенку. Ведь тогда сосуд начал бы двигаться ускоренно без внешних сил, а это противоречит законам механики: освободив закрепленный сосуд со стенками различной температуры, мы не вызовем его смещения. Дело здесь в том, что при данном неравновесном состоянии газа в сосуде концентрация молекул у холодной стенки больше, чем у горячей. Уменьшение кинетической энергии молекул у холодной стенки компенсируется увеличением концентрации молекул и наоборот. В результате давление на холодную и горячую стенки оказывается одним и тем же.

Рассмотрим еще один вариант опыта. Охладим очень быстро одну из стенок. В первый момент давление на нее уменьшится, и сосуд немного сдвинется с места; затем давления выравняются, и сосуд остановится . Но при этом движении центр масс системы останется на месте из-за того, что плотность газа у холодной стенки станет чуть больше, чем у горячей.

Следует отметить, что на самом деле давление не остается строго фиксированной величиной. Оно испытывает флуктуации, и поэтому сосуд слегка «дрожит» на месте. Но амплитуда дрожания сосуда крайне мала.

Итак, окончательно мы пришли к выводу, что давление газа на стенки в сосуде не зависит ни от качества обработки стенок, ни от их температуры.

При выводе уравнения состояния идеального газа будем считать молекулы маленькими твердыми шарами, заключенными в ящик объёмом V (рис. 8.2). Предположение о твердых шарах означает, что между молекулами происходят упругие соударения. Рассмотрим сначала одну такую молекулу, отражающуюся от левой стенки ящика. Средняя сила, действующая на стенку на протяжении времени , равна

В результате соударения импульс изменяется на величину

Поскольку время между соударениями молекулы с этой стенкой

то на стенку со стороны одной молекулы действует средняя сила

Рис. 8.2 Частица в сосуде объёмом lS после отражения от левой стенки

Полная сила, с которой все N молекул в ящике действуют на стенку, дается выражением

где – усредненный по всем частицам квадрат скорости .

Эта величина принято называть среднеквадратичной скоростью в направлении оси X . Разделив обе части этого соотношения на площадь стенки S , получим давление

Заменим S l на объём V ; тогда

Уже отсюда видно, что для данного количества газа произведение pV остается постоянным при условии, что кинетическая энергия частиц сохраняется без изменения. Правую часть формулы (8.16) можно записать через . Действительно,

Поскольку молекулы совершенно одинаково отражаются от всех шести граней, то

Подставим теперь в (8.16) вместо величину :

Мы будем определять абсолютную температуру как величину, прямо пропорциональную средней кинетической энергии молекул в сосуде:

(определение температуры), где – средняя кинетическая энергия, приходящаяся на одну частицу.

Коэффициент пропорциональности (2/ 3k ) представляет собой константу. Значение постоянной k (постоянной Больцмана ) зависит от выбора шкалы температуры. Один из способов выбора шкалы основан на том, что интервал температур между точками кипения и замерзания воды при нормальном давлении полагается равным 100 градусам (=100 К ). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, величина k определяется путем измерения свойств воды. Экспериментально найдено, что

(постоянная Больцмана ). В случае если с помощью (8.18) исключить величину из (8.17), то получим

(уравнение состояния идеального газа ).

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, применив уравнения ньютоновской механики к отдельным молекулам, т. е. использовав их на микроскопическом уровне, мы ввели важное соотношение между макроскопическими величинами p, V и T (ср.
Размещено на реф.рф
(8.20) с (8.7)).

Учитывая равенство (8.20), уравнение состояния идеального газа можно переписать в виде

где n есть концентрация молекул. Так как для одноатомного газа средняя кинетическая энергия совпадает со средней энергией поступательного движения , уравнение (8.21) представим как

Произведение дает суммарную энергию поступательного движения n молекул. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, давление равно двум третям энергии поступательного движения молекул, содержащихся в единице объёма газа.

Где бы ни находился газ: в воздушном шаре, автомобильной шине, или металлическом баллоне - он заполняет собой весь объём сосуда, в котором находится.

Давление газа возникает совсем по другой причине, нежели давление твёрдого тела. Оно образуется в результате ударов молекул о стенки сосуда.

Давление газа на стенки сосуда

Двигаясь хаотично в пространстве, молекулы газа сталкиваются между собой и со стенками сосуда, в котором находятся. Сила удара одной молекулы мала. Но так как молекул очень много, и сталкиваются они с большой частотой, то, действуя сообща на стенки сосуда, они создают значительное давление. Если в газ помещено твёрдое тело, то оно также подвергается ударам молекул газа.

Проведём несложный опыт. Под колокол воздушного насоса поместим завязанный воздушный шарик, не полностью наполненный воздухом. Так как воздуха в нём мало, шарик имеет неправильную форму. Когда же мы начнём откачивать воздух из-под колокола, шарик станет раздуваться. Через некоторое время он примет форму правильного шара.

Что же произошло с нашим шариком? Ведь он был завязан, следовательно, количество воздуха в нём осталось прежним.

Всё объясняется довольно просто. Во время движения молекулы газа сталкиваются с оболочкой шарика снаружи и внутри него. Если воздух откачивается из колокола, молекул становится меньше. Уменьшается плотность, а значит и частота ударов молекул о наружную оболочку также уменьшается. Следовательно, давление снаружи оболочки падает. А так как внутри оболочки число молекул осталось прежним, то внутреннее давление превышает наружное. Газ давит изнутри на оболочку. И по этой причине она постепенно раздувается и принимает форму шара.

Закон Паскаля для газов

Молекулы газа очень подвижны. Благодаря этому давление они передают не только в направлении действия силы, вызывающей это давление, но и равномерно по всем направлениям. Закон о передаче давления сформулировал французский учёный Блез Паскаль: «Давление, производимое на газ или жидкость, передаётся без изменений в любую точку по всем направлениям ». Этот закон называют основным законом гидростатики - науки о жидкости и газе в состоянии равновесия.

Закон Паскаля подтверждается опытом с прибором, который называют шаром Паскаля . Этот прибор представляет собой шар из твёрдого вещества с проделанными в нём крошечными отверстиями, соединённый с цилиндром, по которому двигается поршень. Шар заполняется дымом. При сжатии поршнем дым выталкивается из отверстий шара одинаковыми струйками.

Давление газа вычисляют по формуле:

где е lin - средняя кинетическая энергия поступательного движения молекул газа;

n - концентрация молекул

Парциальное давление. Закон Дальтона

На практике чаще всего нам приходится встречаться не с чистыми газами, а с их смесями. Мы дышим воздухом, являющимся смесью газов. Выхлопные газы автомобилей - тоже смесь. При сварке уже давно не применяется чистый углекислый газ. Вместо него также используют газовые смеси.

Газовой смесью называют смесь газов, не вступающих в химические реакции между собой.

Давление отдельного компонента газовой смеси называется парциальным давлением .

Если предположить, что все газы смеси являются идеальными газами, то давление смеси определяется законом Дальтона: «Давление смеси идеальных газов, не взаимодействующих химически, равно сумме парциальных давлений».

Его величина определяется по формуле:

Каждый газ в смеси создаёт парциальное давление. Его температура равна температуре смеси.

Давление газа можно изменить, меняя его плотность. Чем больше газа будет закачано в металлический баллон, тем больше в нём будет молекул, ударяющихся о стенки, и тем выше станет его давление. Соответственно, откачивая газ, мы разрежаем его, и давление снижается.

Но давление газа также можно изменить, изменив его объём или температуру, то есть, сжав газ. Сжатие проводят, воздействуя силой на газообразное тело. В результате такого воздействия уменьшается занимаемый им объём, повышается давление и температура.

Газ сжимается в цилиндре двигателя при движении поршня. На производстве высокое давление газа создают, сжимая его с помощью сложных устройств - компрессоров, которые способны создать давление до нескольких тысяч атмосфер.